Law of sines: Difference between revisions
Jump to navigation
Jump to search
imported>David E. Volk (New page: The law of sines is useful for calculating one side or angle of any triangle, when five of the six angles and sides are known. <math> \left(\frac{sin {A}}{a}\right) = \left(\frac{sin {...) |
imported>Michael Underwood No edit summary |
||
| Line 1: | Line 1: | ||
In [[geometry]] the '''law of sines''' is useful for calculating one side or angle of any triangle, when five of the six angles and sides are known. It can be stated as | |||
<math> | :<math> \frac{\sin {A}}{a} = \frac{\sin {B}}{b} = \frac{\sin{C}}{c} </math> | ||
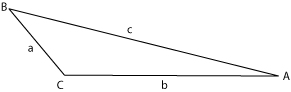
where the lengths <math>a</math>, <math>b</math>, and <math>c</math> correspond to the sides opposite the respective angles <math>A</math>, <math>B</math>, and <math>C</math> as shown in the image. | |||
[[Image:Triangle.jpg|center|frame|Triangle]] | [[Image:Triangle.jpg|center|frame|Triangle]] | ||
[[Category:CZ Live]] | [[Category:CZ Live]] | ||
[[Category:Mathematics Workgroup]] | [[Category:Mathematics Workgroup]] | ||
Revision as of 17:41, 3 October 2007
In geometry the law of sines is useful for calculating one side or angle of any triangle, when five of the six angles and sides are known. It can be stated as
where the lengths , , and correspond to the sides opposite the respective angles , , and as shown in the image.