Faraday's law (electromagnetism): Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 6: | Line 6: | ||
\Phi \equiv \iint_{S} \mathbf{B}\cdot d\mathbf{S}, | \Phi \equiv \iint_{S} \mathbf{B}\cdot d\mathbf{S}, | ||
</math> | </math> | ||
where d'''''S''''' is a vector normal to the infinitesimal surface element d''S'' and of length d''S''. | where d'''''S''''' is a vector normal to the infinitesimal surface element d''S'' and d'''''S''''' is of length d''S''. | ||
The dot stands for the [[inner product]] between the magnetic induction '''B''' and d'''''S'''''. | The dot stands for the [[inner product]] between the magnetic induction '''B''' and d'''''S'''''. In vacuum the magnetic induction '''B''' is proportional to the magnetic field '''H'''. (In SI units: '''B''' = μ<sub>0</sub> '''H''' with μ<sub>0</sub> the [[magnetic constant]] of the vacuum; in Gaussian units: '''B''' = '''H'''.) | ||
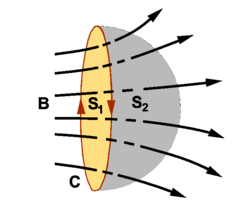
The flux through two surfaces that together form a closed surface is equal because of [[Gauss' law (magnetism)|Gauss' law]]. Indeed, in the figure on the right the surfaces ''S''<sub>1</sub> and ''S''<sub>2</sub>, which have the boundary ''C'' in common, form together a closed surface. Hence Gauss' law states that | The flux through two surfaces that together form a closed surface is equal because of [[Gauss' law (magnetism)|Gauss' law]]. Indeed, in the figure on the right the surfaces ''S''<sub>1</sub> and ''S''<sub>2</sub>, which have the boundary ''C'' in common, form together a closed surface. Hence Gauss' law states that | ||
| Line 15: | Line 15: | ||
where the minus sign of the first term is due to the fact that the flux is ''into'' the volume enveloped by the two surfaces. It follows that | where the minus sign of the first term is due to the fact that the flux is ''into'' the volume enveloped by the two surfaces. It follows that | ||
:<math> | :<math> | ||
\Phi = \iint_{S_1} \mathbf{B}\cdot d\mathbf{S} = \iint_{S_2} \mathbf{B}\cdot d\mathbf{S} | \Phi = \iint_{S_1} \mathbf{B}\cdot d\mathbf{S} = \iint_{S_2} \mathbf{B}\cdot d\mathbf{S}, | ||
</math> | </math> | ||
and that the magnetic flux Φ can be computed with respect to ''any'' surface that has ''C'' as boundary. | |||
The electromotive force (EMF)<ref>The term EMF has historical origin, but is somewhat unfortunate as it is not a force but a potential.</ref> is defined as | The electromotive force (EMF)<ref>The term EMF has historical origin, but is somewhat unfortunate as it is not a force but a potential.</ref> is defined as | ||
| Line 26: | Line 27: | ||
Faraday's law of magnetic induction relates the EMF <math>\scriptstyle \mathcal{E} </math> to the time derivative of the magnetic flux, it reads: | Faraday's law of magnetic induction relates the EMF <math>\scriptstyle \mathcal{E} </math> to the time derivative of the magnetic flux, it reads: | ||
:<math> | :<math> | ||
\mathcal{E} = - \frac{d \Phi}{dt} | \mathcal{E} = - k \frac{d \Phi}{dt} \quad \textrm{with}\quad | ||
k= | |||
\begin{cases} | |||
1 \quad & \hbox{SI units} \\ | |||
1/c &\hbox{Gaussian units}, | |||
\end{cases} | |||
</math> | </math> | ||
If ''C'' is a | where ''c'' is the speed of light. If ''C'' is a conducting loop, then under influence of the EMF a current ''i''<sub>ind</sub> will run through it. The minus sign in Faraday's law has the consequence that the magnetic field generated by | ||
''i''<sub>ind</sub> opposes the change in | ''i''<sub>ind</sub> opposes the change in Φ this phenomenon is known as [[Lenz' law]]. If the surface ''S'' is constant the change in Φ is solely due to a change in '''B'''. | ||
Faraday's law forms the theoretical basis of the [[electric motor]], the [[dynamo]], and the [[electric generator]]. | |||
==Note== | ==Note== | ||
Revision as of 01:54, 16 May 2008
In electromagnetism Faraday's law of magnetic induction states that a change in magnetic flux generates an electromotive force. The law is named after the English scientist Michael Faraday.
The magnetic flux Φ through a surface S is defined as the surface integral
where dS is a vector normal to the infinitesimal surface element dS and dS is of length dS. The dot stands for the inner product between the magnetic induction B and dS. In vacuum the magnetic induction B is proportional to the magnetic field H. (In SI units: B = μ0 H with μ0 the magnetic constant of the vacuum; in Gaussian units: B = H.)
The flux through two surfaces that together form a closed surface is equal because of Gauss' law. Indeed, in the figure on the right the surfaces S1 and S2, which have the boundary C in common, form together a closed surface. Hence Gauss' law states that
where the minus sign of the first term is due to the fact that the flux is into the volume enveloped by the two surfaces. It follows that
and that the magnetic flux Φ can be computed with respect to any surface that has C as boundary.
The electromotive force (EMF)[1] is defined as
where the electric field E is integrated around the closed path C.
Faraday's law of magnetic induction relates the EMF to the time derivative of the magnetic flux, it reads:
where c is the speed of light. If C is a conducting loop, then under influence of the EMF a current iind will run through it. The minus sign in Faraday's law has the consequence that the magnetic field generated by iind opposes the change in Φ this phenomenon is known as Lenz' law. If the surface S is constant the change in Φ is solely due to a change in B.
Faraday's law forms the theoretical basis of the electric motor, the dynamo, and the electric generator.
Note
- ↑ The term EMF has historical origin, but is somewhat unfortunate as it is not a force but a potential.
(To be continued)