Periodic function: Difference between revisions
Jump to navigation
Jump to search

imported>Michael Underwood No edit summary |
mNo edit summary |
||
| (5 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
In [[mathematics]] a | {{subpages}} | ||
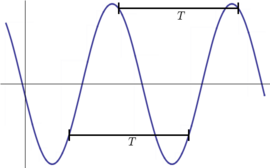
[[Image:periodicFunction.png|thumb|270px|Example of a periodic function, with period <math>T</math>. If you choose any point on the function and then move to the left or right by <math>T</math>, you will find the same value as at the original point.]] | |||
In [[mathematics]] a '''periodic function''' is a [[function]] that repeats itself after a while, and indefinitely. | |||
The mathematical definition of this is that <math>f(t)</math> is periodic with [[period]] <math>T</math> | The mathematical definition of this is that <math>f(t)</math> is periodic with [[period]] <math>T</math> | ||
if | if | ||
: <math>f(t+T)=f(t)\ \ \forall\ t\in\mathbb{R}\ .</math> | : <math>f(t+T)=f(t)\ \ \forall\ t\in\mathbb{R}\ .</math> | ||
Common examples of periodic functions are <math>\sin(\omega t)</math> and <math>\cos(\omega t)</math>, which both | |||
have period <math>2\pi/\omega</math>. | |||
A sawtooth wave is a periodic function that can be described by | |||
: <math> f(x) = \begin{cases} |x-1| & \text{if } -1<x<1, \\ f(x+2) & \text{if } x \le -1, \\ f(x-2) & \text{if } x \ge 1. \end{cases} </math>[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 17:01, 2 October 2024
In mathematics a periodic function is a function that repeats itself after a while, and indefinitely. The mathematical definition of this is that is periodic with period if
Common examples of periodic functions are and , which both have period .
A sawtooth wave is a periodic function that can be described by