Superfunction: Difference between revisions

From Citizendium
Jump to navigation Jump to search
imported>Dmitrii Kouznetsov
mNo edit summary
 
(22 intermediate revisions by 4 users not shown)
Line 7: Line 7:
then <math>S</math> can be interpreted as superfunction of function <math>f</math>.
then <math>S</math> can be interpreted as superfunction of function <math>f</math>.
Such definition is valid only for positive integer <math>z</math>.  
Such definition is valid only for positive integer <math>z</math>.  
The most research and appllications around the superfunctions is related with various extensions of superfunction; and analysis of the existence, uniqueness and ways of the evaluation.
The most research and applications around the superfunctions are related with various extensions of superfunction; and analysis of the existence, uniqueness and ways of the evaluation.
<!--  In particular, :<math>S(1)=f(t)</math> !-->
<!--  In particular, :<math>S(1)=f(t)</math> !-->
For simple function <math>f</math>, such as addition of a constant or multiplication by a constant,
For simple function <math>f</math>, such as addition of a constant or multiplication by a constant,
Line 48: Line 48:
the <math>\sqrt{\exp}</math> was more lucky than the <math>~\sqrt{!~}~~</math>; at least the existence of [[holomorphic function]]  
the <math>\sqrt{\exp}</math> was more lucky than the <math>~\sqrt{!~}~~</math>; at least the existence of [[holomorphic function]]  
<math>\varphi</math> such that <math>\varphi(\varphi(z))=\exp(z)</math> has been demonstrated in 1950 by [[Helmuth Kneser]] <ref name="kneser">
<math>\varphi</math> such that <math>\varphi(\varphi(z))=\exp(z)</math> has been demonstrated in 1950 by [[Helmuth Kneser]] <ref name="kneser">
H.Kneser. “Reelle analytische L¨osungen der Gleichung <math>\varphi(\varphi(x)) = e^x </math> und verwandter Funktionalgleichungen”.
{{cite journal
Journal fur die reine und angewandte Mathematik, 187 (1950), 56-67.
|author=[[Helmuth Kneser|H.Kneser]]
</ref>. Actually, for his proof, Kneser had constructed the superfunction of exp and corresponding Abel function <math>\mathcal{X}</math>, satisfying the [[Abel equation]]
|title=Reelle analytische L¨osungen der Gleichung <math>\varphi(\varphi(x)) = e^x </math> und verwandter Funktionalgleichungen
: <math>\mathcal{X}(\exp(z))=\mathcal{X}(z)+1</math>
|journal=[[Journal fur die reine und angewandte Mathematik]]
the inverse function, ide est <math>F=\mathcal \chi^{-1}</math> is an [[entire function|entire]] super-exponential, although it is not real at the real axis; it cannot be interpreted as [[tetration]], because the condition <math>F(0)=1</math> cannot be realized for the entire super-exponential. The [[real function|real]] <math>\sqrt{\exp}</math> can be constructed with the [[tetration|tetrational]] (which is a superexponential), and the real <math>\sqrt{\rm Factorial}</math> can be constructed with the [[superfactorial]]. The plots of <math>\sqrt{\rm Factorial}</math> and <math>\sqrt{\exp}</math> in the compex plane are shown in the right hand side figure.
|volume=187
|year=1950
|pages=56-67}}
</ref>. Actually, for his proof, Kneser had constructed the superfunction of exp and the corresponding Abel function <math>\mathcal{X}</math>, satisfying the [[Abel equation]]
: <math>\mathcal{X}(\exp(z))=\mathcal{X}(z)+1</math> .
The inverse function, id est <math>F=\mathcal \chi^{-1}</math> is an [[entire function|entire]] super-exponential, although it is not real at the real axis; it cannot be interpreted as [[Tetration|tetrational]], because the condition <math>F(0)=1</math> cannot be realized for the entire super-exponential. The [[real function|real]] <math>\sqrt{\exp}</math> can be constructed with the [[tetration|tetrational]] (which is also a superexponential), and the real <math>\sqrt{\rm Factorial}</math> can be constructed with the [[superfactorial]]. The plots of <math>\sqrt{\rm Factorial}</math> and <math>\sqrt{\exp}</math> in the complex plane are shown in the right hand side figure.


==Extensions==
==Extensions==
The recurrence above can be written as equations
The recurrent formula of the preamble can be written as equations
:<math>S(z\!+\!1)=f(S(z)) ~ \forall z\in \mathbb{N} : z>0</math>
:<math>S(z\!+\!1)=f(S(z)) ~ \forall z\in \mathbb{N} : z>0</math>
:<math>S(1)=f(t)</math>.
:<math>S(1)=f(t)</math>.
Line 66: Line 71:
The following extension, for example,
The following extension, for example,
:<math>S(-2)=f^{-2}(t)</math>  
:<math>S(-2)=f^{-2}(t)</math>  
is not trifial, because the inverse function may happen to be not defined for some values of <math>t</math>.
is not trivial, because the inverse function may happen to be not defined for some values of <math>t</math>.
In particular, [[tetration]] can be interpreted as super-function of exponential for some real base <math>b</math>; in this case,
In particular, [[tetration]] can be interpreted as super-function of exponential for some real base <math>b</math>; in this case,
<!-- :<math>f(z)={b}^z</math>!-->
<!-- :<math>f(z)={b}^z</math>!-->
Line 122: Line 127:


==Examples==
==Examples==
The short table of superfunctions is suggested in
<ref name="superfactorial">
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. [[Moscow University Physics Bulletin]], 2010, v.65, No.1, p.6-12. (Preprint ILS UEC, 2009:
http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf )
</ref>. A little bit more extended table is available at [[TORI]]
<ref name="toritable">
http://tori.ils.uec.ac.jp/TORI/index.php/Table_of_superfunctions
</ref>. Some superfunctions can be expressed with elementary functions,
they are used without to mention that they are superfunctions.
For example, for the transfer function "++", which means unity increment,
the superfunction is just addition of a constant.
===Addition===
===Addition===
Chose a [[complex number]] <math>c</math> and define function  
Chose a [[complex number]] <math>c</math> and define function  
Line 156: Line 173:
<ref name="mueller">Mueller. Problems in Mathematics.
<ref name="mueller">Mueller. Problems in Mathematics.
http://www.math.tu-berlin.de/~mueller/projects.html
http://www.math.tu-berlin.de/~mueller/projects.html
</ref>.
More general case refers to the [[logistic transfer function]] <math> H(z)=u~z~(1-z) </math>
where <math>u>1</math> is parameter; the corresponding superfunction <math>F</math> is called [[logistic sequence]]
<ref name="logistic">
{{cite journal
|url=http://www.springerlink.com/content/u712vtp4122544x4/
|first=Dmitrii
|last=Kouznetsov
|title=Holomorphic extension of the logistic sequence
|journal=[[Moscow University Physics Bulletin]]
|year=2010
|issue=2
|pages=91-98
}}</ref>; <math>F(z\!+\!1)=H(F(z))</math>.
Within wide range of values of parameter <math>u</math>, the logistic sequence <math> H(z)</math> is holomorphic function of <math>z</math>; at <math>u\!=\!4</math>, it can be expressed in a way, equivalent to the representation above <ref name="superfactorial"/>
<!--<ref name="logistic">
{{cite journal
|url=http://www.springerlink.com/content/u712vtp4122544x4/
|first=Dmitrii
|last=Kouznetsov
|title=Holomorphic extension of the logistic sequence
|journal=[[Moscow University Physics Bulletin]]
|year=2010
|issue=2
|pages=91-98
}}
</ref>
</ref>
Should it be cited again?
!-->
.
===Rational function===
===Rational function===
In general, the transfer function <math>H</math> has no  need to be [[entire function]].
In general, the transfer function <math>H</math> has no  need to be [[entire function]].
Line 225: Line 273:
[[Image:Sqrt(exp)(z).jpg|200px|right|thumb|<math>\exp^c</math> in the complex plane for various <math>c</math>]]
[[Image:Sqrt(exp)(z).jpg|200px|right|thumb|<math>\exp^c</math> in the complex plane for various <math>c</math>]]


A superfunction <math>S</math> allow to calculate the fractional iteration <math>H^c</math> of some transfer function <math>H</math>. Once the superfunction <math>S</math> and the [[Abel function]] <math>A=S^{-1}</math> are established,  
A superfunction <math>S</math> allows to calculate the fractional iteration <math>H^c</math> of some transfer function <math>H</math>. Once the superfunction <math>S</math> and the [[Abel function]] <math>A=S^{-1}</math> are established,  
The fractional iteration can be defined as  
the fractional iteration can be defined as  
<math>H^c(z)=S(c+A(z))</math>. Then, as <math>c</math> changes from 1 to <math>-1</math>, the holomorphic transition from function <math>H</math> to <math>H^{-1}</math> is relalised. The figure at left shows an example of transition from  
<math>H^c(z)=S(c+A(z))</math>. Then, as <math>c</math> changes from 1 to <math>-1</math>, the holomorphic transition from function <math>H</math> to <math>H^{-1}</math> is relalised. The figure at left shows an example of transition from  
<math>\exp^{1}\!=\!\exp </math> to  
<math>\exp^{1}\!=\!\exp </math> to  
<math>\exp^{\!-1}\!=\!\ln </math>.
<math>\exp^{\!-1}\!=\!\ln </math>.
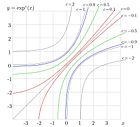
Function <math>\exp^c</math> versus real argument is shown for
Function <math>\exp^c</math> versus real argument is plotted for
<math>c=2,1,0.9, 0.5, 0.1, -0.1,-0.5, -0.9, -1,-2</math>. The [[tetration]]al and ArcTetrational were used as superfunction  
<math>c=2,1,0.9, 0.5, 0.1, -0.1,-0.5, -0.9, -1,-2</math>. The [[tetration]]al and ArcTetrational were used as superfunction  
<math>S</math>
<math>S</math>
Line 236: Line 284:
The figure at right shows these functions in the complex plane.
The figure at right shows these functions in the complex plane.
At non-negative integer number of iteration, the iterated exponential is [[entire function]]; at non-integer values, it has two [[branch points]], thich correspond to the [[fixed points]] <math>L</math> and
At non-negative integer number of iteration, the iterated exponential is [[entire function]]; at non-integer values, it has two [[branch points]], thich correspond to the [[fixed points]] <math>L</math> and
<math>L^*</math> of natural logarithm. However, <math>\exp^c(z)</math> remains [[holomorphic function|holomorphic]] at least in the strip <math>|\Im(z)|<\Im(L)\approx 1.3 </math> along the real axis.
<math>L^*</math> of natural logarithm. At <math>c\!\ge\! 0</math>, function <math>\exp^c(z)</math> remains [[holomorphic function|holomorphic]] at least in the strip <math>|\Im(z)|<\Im(L)\approx 1.3 </math> along the real axis.


===Nonlinear Optics===
===Nonlinear Optics===
Line 249: Line 297:
Transfer Function of the similar sample, which is half thiner,
Transfer Function of the similar sample, which is half thiner,
could be interpreted as the square root (id est, half-iteration) of the Transfer Function of the initial sample.
could be interpreted as the square root (id est, half-iteration) of the Transfer Function of the initial sample.
Similar example is suggested for a nonlinear optical fiber <ref name="kouznetsov">
{{cite journal
|author=D.Kouznetsov.
|title=Solutions of <math>F(z+1)=\exp(F(z))</math> in the complex <math>z</math>plane.
|journal=[[Mathematics of Computation]],
|year=2009
|volume=78
|pages=1647-1670
|url= http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
|preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/analuxp99.pdf
|doi=10.1090/S0025-5718-09-02188-7
}}</ref>.


===Nonlinear Acoustics===
===Nonlinear Acoustics===
Line 258: Line 319:
may be boosted with the superfunction.
may be boosted with the superfunction.


===Vaporation and condensation===
===Vaporization and condensation===
<!--For the separation of isotopes due to the different pressure of the saturated vapor for different components,!-->
<!--For the separation of isotopes due to the different pressure of the saturated vapor for different components,!-->
In analysis of condensation, the growth (or vaporization) of a small drop of liquid can be considered,
In analysis of condensation, the growth (or vaporization) of a small drop of liquid can be considered,
Line 281: Line 342:


==References==
==References==
<references/>
{{reflist}}[[Category:Suggestion Bot Tag]]

Latest revision as of 11:01, 23 October 2024

This article is developing and not approved.
 Main Article
 Discussion
Related Articles  [?]
Bibliography  [?]
External Links  [?]
Citable Version  [?]
 
https://en.citizendium.org/wiki/index.php?title=Superfunction&printable=yes
This editable Main Article is under development and subject to a disclaimer.

Superfunction comes from iteration of another function. Roughly, for some function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} and for some constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} , the superfunction could be defined with expression

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {{S(z)} \atop \,} {= \atop \,} {{\underbrace{f\Big(f\big(... f(t)...\big)\Big)}} \atop {z \mathrm{~evaluations~of~function~}f\! \!\!\!\!\!}}}

then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} can be interpreted as superfunction of function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} . Such definition is valid only for positive integer Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} . The most research and applications around the superfunctions are related with various extensions of superfunction; and analysis of the existence, uniqueness and ways of the evaluation. For simple function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} , such as addition of a constant or multiplication by a constant, the superfunction can be expressed in terms of elementary function. In particular, the Ackernann functions and tetration can be interpreted in terms of super-functions.

History

logos of the Phys.Dept. of the MSU and that of Math.Dep.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{!}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\exp}} in the complex plane

Analysis of superfunctions came from the application to the evaluation of fractional iterations of functions. Superfunctions and their inverse functions allow evaluation of not only minus-first power of a function (inverse function), but also any real and even complex iteration of the function. Historically, the first function of such kind considered was Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\exp}~} ; then, function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{!~}~} was used as logo of the Physics department of the Moscow State University [1][2][3]. (Mathematicians of the same University were not so arrogant and used the symbol of integral and the Moebius surface at their logo, see the figure at left).

That time, researchers did not have computational facilities for evaluation of such functions, but the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\exp}} was more lucky than the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ~\sqrt{!~}~~} ; at least the existence of holomorphic function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi(\varphi(z))=\exp(z)} has been demonstrated in 1950 by Helmuth Kneser [4]. Actually, for his proof, Kneser had constructed the superfunction of exp and the corresponding Abel function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{X}} , satisfying the Abel equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{X}(\exp(z))=\mathcal{X}(z)+1} .

The inverse function, id est Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=\mathcal \chi^{-1}} is an entire super-exponential, although it is not real at the real axis; it cannot be interpreted as tetrational, because the condition Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(0)=1} cannot be realized for the entire super-exponential. The real Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\exp}} can be constructed with the tetrational (which is also a superexponential), and the real Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\rm Factorial}} can be constructed with the superfactorial. The plots of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\rm Factorial}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\exp}} in the complex plane are shown in the right hand side figure.

Extensions

The recurrent formula of the preamble can be written as equations

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(z\!+\!1)=f(S(z)) ~ \forall z\in \mathbb{N} : z>0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(1)=f(t)} .

Instead of the last equation, one could write

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(0)=t}

and extend the range of definition of superfunction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} to the non-negative integers. Then, one may postulate

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(-1)=f^{-1}(t)}

and extend the range of validity to the integer values larger than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2} . The following extension, for example,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(-2)=f^{-2}(t)}

is not trivial, because the inverse function may happen to be not defined for some values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} . In particular, tetration can be interpreted as super-function of exponential for some real base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} ; in this case,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=\exp_{b}}

then, at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=1} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(-1)=\log_b(1)=0 } .

but

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(-2)=\log_b(0)~ \mathrm{is~ not~ defined}} .

For extension to non-integer values of the argument, superfunction should be defined in different way.

Definition

For complex numbers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ~a~} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ~b~} , such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ~a~} belongs to some connected domain Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D\subseteq \mathbb{C}} ,
superfunction (from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} ) of holomorphic function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ~f~} on domain Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} is function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S } , holomorphic on domain Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} , such that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(z\!+\!1)=f(S(z)) ~ \forall z\in D : z\!+\!1 \in D}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(a)=b} .

Uniqueness

In general, the super-function is not unique. For a given base function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} , from given Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a\mapsto d)} superfunciton , another super-function could be constructed as

where is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that .

The modified super-function may have narrowed range of holomorphism. The variety of possible super-functions is especially large in the limiting case, when the width of the range of holomorphizm becomes zero; in this case, one deals with the real-analytic superfunctions [5].

If the range of holomorphism required is large enough, then, the super-function is expected to be unique, at least in some specific base functions . In particular, the super-function of , for , is called tetration and is believed to be unique at least for ; for the case , see [6]; but up to year 2009, the uniqueness is rather conjecture than a theorem with the formal mathematical proof.

Examples

The short table of superfunctions is suggested in [7]. A little bit more extended table is available at TORI [8]. Some superfunctions can be expressed with elementary functions, they are used without to mention that they are superfunctions. For example, for the transfer function "++", which means unity increment, the superfunction is just addition of a constant.

Addition

Chose a complex number and define function with relation . Define function with relation .

Then, function is superfunction ( to ) of function on .

Multiplication

Exponentiation is superfunction (from 1 to ) of function .

Quadratic polynomials

Let . Then, is a superfunction of .

Indeed,

and

In this case, the superfunction is periodic; its period

and the superfunction approaches unity also in the negative direction of the real axis,

The example above and the two examples below are suggested at [9].

More general case refers to the logistic transfer function where is parameter; the corresponding superfunction is called logistic sequence [10]; . Within wide range of values of parameter , the logistic sequence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(z)} is holomorphic function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} ; at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u\!=\!4} , it can be expressed in a way, equivalent to the representation above [7] .

Rational function

In general, the transfer function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} has no need to be entire function. Here is the example with meromorphic function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} . Let

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(z)=\frac{2z}{1-z^2} ~ \forall z\in D~} ; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ~ D=\mathbb{C} \backslash \{-1,1\}}

Then, function

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z)=\tan(\pi 2^z)}

is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (C, 0\! \mapsto\! 0)} superfunction of function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} is the set of complex numbers except singularities of function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} . For the proof, the trigonometric formula

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan(2 \alpha)=\frac{2 \tan(\alpha)}{1-\tan(\alpha)^2}~~ \forall \alpha \in \mathbb{C} \backslash \{\alpha\in \mathbb{C} : \cos(\alpha)=0 || \sin(\alpha)=\pm \cos(\alpha) \} }

can be used at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha=\pi 2^z } , that gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(F(z))=\frac{2 \tan(\pi 2^z)}{1-\tan(\pi 2^z)} = \tan(2 \pi 2^z)=F(z+1) }

Algebraic function

In the similar way one can consider the transfer function

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(z)=2z \sqrt{1-z^2}}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z)=\sin(\pi 2^z)}

which is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (C,~ 0\!\rightarrow \!0)} superfunction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C= \{z\in \mathbb C : \Re( \cos(\pi 2^z))>0 \}} .

Exponentiation

Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b>1} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(z)= \exp_b(z)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C= \{ z \in \mathbb{C} : \Re(z)>-2 \}} . Then, tetration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{tet}_b } is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (C,~ 0\! \rightarrow\! 1)} superfunction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \exp_b} .

Abel function

Inverse of superfunction can be interpreted as the Abel function.

For some domain Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\subseteq \mathbb{C}} and some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u\in E} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v\in \mathbb{C}} ,
Abel function (from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v } ) of function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} with respect to superfunction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} on domain Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E \in \mathbb{C}} is holomorphic function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} such that

The definitionm above does not reuqire that ; although, from properties of holomorphic functions, there should exist some subset such that . In this subset, the Abel function satisfies the Abel equation.

Abel equation

The Abel equation is some equivalent of the recurrent equation

in the definition of the superfunction. However, it may hold for from the reduced domain .

Applications of superfunctions and the Abel functions

Superfunctions, usially the superexponentials, are proposed as a fast-growing function for an upgrade of the floating point representation of numbers in computers. Such an upgrade would greatly extend the range of huge numbers which are still distinguishable from infinity.

Other applications refer to the calculation of fractional iterates (or fractional power) of a function. Any holomorphic function can be declared as a "transfer function", then its superfunctions and corresponding Abel functions can be considered.

Transition from a function to its inverse function

versus for various
in the complex plane for various

A superfunction allows to calculate the fractional iteration of some transfer function . Once the superfunction and the Abel function are established, the fractional iteration can be defined as . Then, as changes from 1 to , the holomorphic transition from function to is relalised. The figure at left shows an example of transition from to . Function versus real argument is plotted for . The tetrational and ArcTetrational were used as superfunction and Abel function of the exponential. The figure at right shows these functions in the complex plane. At non-negative integer number of iteration, the iterated exponential is entire function; at non-integer values, it has two branch points, thich correspond to the fixed points and of natural logarithm. At , function remains holomorphic at least in the strip along the real axis.

Nonlinear Optics

In the investigation of the nonlinear response of optical materials, the sample is supposed to be optically thin, in such a way, that the intensity of the light does not change much as it goes through. Then one can consider, for example, the absorption as function of the intensity. However, at small variation of the intensity in the sample, the precision of measurement of the absorption as function of intensity is not good. The reconstruction of the superfunction from the Transfer Function allows to work with relatively thick samples, improving the precision of measurements. In particular, the Transfer Function of the similar sample, which is half thiner, could be interpreted as the square root (id est, half-iteration) of the Transfer Function of the initial sample.

Similar example is suggested for a nonlinear optical fiber [6].

Nonlinear Acoustics

It may have sense to characterize the nonlinearities in the attenuation of shock waves in a homogeneous tube. This could find an application in some advanced muffler, using nonlinear acoustic effects to withdraw the energy of the sound waves without to disturb the flux of the gas. Again, the analysis of the nonlinear response, id est, the Transfer Function, may be boosted with the superfunction.

Vaporization and condensation

In analysis of condensation, the growth (or vaporization) of a small drop of liquid can be considered, as it diffuses down through a tube with some uniform concentration of vapor. In the first approximation, at fixed concentration of the vapor, the mass of the drop at the output end can be interpreted as the Transfer Function of the input mass. The square root of this Transfer Function will characterize the tube of half length.

Snow avalanche

The mass of a snowball, that rolls down from the hill, can be considered as a function of the path it already have passed. At fixed length of this path (that can be determined by the altitude of the hill) this mass can be considered also as a Transfer Function of the input mass. The mass of the snowball could be measured at the top of the hill and at thе bottom, giving the Transfer Function; then, the mass of the snowball as a function of the length it passed is superfunction.

Operational element

If one needs to build-up an operational element with some given transfer function , and wants to realize it as a sequential connection of a couple of identical operational elements, then, each of these two elements should have transfer function . Such a function can be evaluated through the superfunction and the Abel function of the transfer function .

The operational element may have any origin: it can be realized as an electronic microchip, or a mechanical couple of curvilinear grains), or some asymmetric U-tube filled with different liquids, and so on.

References

  1. ↑ Logo of the Physics Department of the Moscow State University. (In Russian); http://zhurnal.lib.ru/img/g/garik/dubinushka/index.shtml
  2. ↑ V.P.Kandidov. About the time and myself. (In Russian) http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf:

    По итогам студенческого голосования победителями оказались значок с изображением

    рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом кафедры биофизики А.Сарвазяном, привлекал своей простотой и выразительностью. Тогда эмблема этого значка подверглась жесткой критике со стороны руководства факультета, поскольку она не имеет физического смысла, математически абсурдна и идеологически бессодержательна.

  3. ↑ 250 anniversary of the Moscow State University. (In Russian) ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! http://nauka.relis.ru/11/0412/11412002.htm

    На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее.

  4. ↑ H.Kneser (1950). "Reelle analytische L¨osungen der Gleichung und verwandter Funktionalgleichungen". Journal fur die reine und angewandte Mathematik 187: 56-67.
  5. ↑ P.Walker (1991). "Infinitely differentiable generalized logarithmic and exponential functions". Mathematics of computation 196: 723-733.
  6. ↑ 6.0 6.1 D.Kouznetsov. (2009). "Solutions of in the complex plane.". Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7. Research Blogging.
  7. ↑ 7.0 7.1 D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Preprint ILS UEC, 2009: http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf )
  8. ↑ http://tori.ils.uec.ac.jp/TORI/index.php/Table_of_superfunctions
  9. ↑ Mueller. Problems in Mathematics. http://www.math.tu-berlin.de/~mueller/projects.html
  10. ↑ Kouznetsov, Dmitrii (2010). "Holomorphic extension of the logistic sequence". Moscow University Physics Bulletin (2): 91-98.
Retrieved from "https://citizendium.org/wiki/index.php?title=Superfunction&oldid=989728"