Taylor series: Difference between revisions
imported>Charles Blackham (exp & ln) |
mNo edit summary |
||
| (15 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
'''Taylor series''' | {{subpages}} | ||
A '''Taylor series''' is an infinite sum of polynomial terms to approximate a function in the region about a certain point <math>a</math>. This is only possible if the function is behaving analytically in this neighbourhood. Such series about the point <math>a=0</math> are known as '''Maclaurin series''', after Scottish mathematician Colin Maclaurin. They work by ensuring that the approximate series matches up to the n<sup>th</sup> derivative of the function being approximated when it is approximated by a polynomial of degree <math>n</math>. | |||
==Proof== | ==Proof== | ||
| Line 6: | Line 8: | ||
==Series== | ==Series== | ||
===General formula=== | ===General formula=== | ||
An intuitive explanation of the Taylor series is that, in order to approximate the value of <math>f(x)</math>, as a first approximation we use the value at another point <math>a</math>, i.e. <math>f(a)</math>. If <math>x</math> and <math>a</math> are close together and <math>f</math> varies only slowly, this can be a good approximation. Then we refine the approximation step by step. The derivative of <math>f</math> is used to calculate approximately how much <math>f</math> would be expected to change between <math>a</math> and <math>x</math>, and this amount is added as a correction. But we assume we only know the derivative of <math>f</math> at <math>a</math>, and the derivative may change between the two numbers, so another correction is needed, involving the second derivative which is a measure of how much the first derivative changes. So it continues, adding corrections to corrections, and in the limit, if it converges then it converges to the actual value of <math>f(x)</math> even if <math>x</math> and <math>a</math> are far apart. | |||
:<math> | :<math> | ||
f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\cdots+\frac{f^{(r)}(a)}{r!}(x-a)^r+\cdots | f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\cdots+\frac{f^{(r)}(a)}{r!}(x-a)^r+\cdots | ||
</math> | </math> | ||
::<math>=\sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!} (x-a)^{n}</math> | ::<math>=\sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!} (x-a)^{n}</math> | ||
where <math>\scriptstyle f'</math> is the first derivative of the function <math>\scriptstyle f</math>, and <math>\scriptstyle f''</math> is the second derivative, and so on. Most practically used smooth functions satisfy this formula but not all of them. The smooth function <math>f(x)=\exp(-1/x^2)</math> have all derivatives equal to zero but the function itself is not equal to zero. In order to prove Taylor formula for particular functions, mathematicians reduce the problem to proving Taylor formula for basic functions using a variety of theorems. Taylor formula for basic functions can be proved directly by estimating their derivatives. | |||
==Convergence of the Taylor series and examples== | |||
Region of convergence of the Taylor series is always circle. This circle is centered at the point of expansion. | |||
Radius of this circle is equal to the distance from this point to the closest singulatiry. Within the circle of convergence, | |||
the Taylor series can be used to make the [[polynomial approximation]] of [[holomorphic function]]s, just truncating the series. | |||
=== f(z)=1/z === | |||
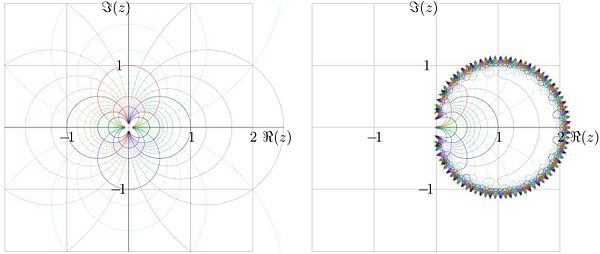
{{Image|TaylorExampleZ.jpg|right|600px|Function <math>f=1/z</math> and its approximation made of the Taylor series at point <math>z=1</math> in the complex <math>z</math> plane.}} | |||
The simple function, which is not polynomoal, is <math>f=1/z</math> This function is shown in the left hand side of the figure in the complex <math>z</math> plane with lines of constant <math>\Re(f)</math> and constant <math>\Im(f)</math>. The polynomial approximation of this function can be obtained truncating the Taylor series; for example, taking 21 terms of the Taylor series developed at <math>z=1</math> gives the approximation | |||
:<math> t_{20}(z)=\sum_{n=0}^{20} (1-z)^n</math> | |||
This function is shown in the right hand side of the figure. In the central part of the circle of convergence, the | |||
truncated Taylor series approximate the function. | |||
Below, more example of Taylor series of various functions are suggested. | |||
===Exponential & Logarithmic functions=== | ===Exponential & Logarithmic functions=== | ||
:<math> | :<math> | ||
e^x=1+x+\frac{x^2 | e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots+\frac{x^r}{r!}+\cdots \qquad \forall x \in \mathbb{C} | ||
</math><br/><br/> | </math><br/><br/> | ||
:<math> | :<math> | ||
ln(1+x)=x-\frac{x^2 | \ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots+(-1)^{r+1}\frac{x^r}{r}+\cdots \qquad | ||
\forall x \in \mathbb{C}: |x|\le 1 , x\ne -1 | |||
</math> | </math> | ||
===Trigonometric functions=== | ===Trigonometric functions=== | ||
:<math> | |||
\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+(-1)^{r}\frac{x^{2r+1}}{(2r+1)!}+\cdots \qquad \forall x | |||
</math><br/><br/> | |||
:<math> | |||
\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots+(-1)^{r}\frac{x^{2r}}{(2r)!}+\cdots \qquad \forall x | |||
</math><br/><br/> | |||
:<math> | |||
\tan x=x+\frac{x^3}{3}+\frac{2 x^5}{15}+\cdots+\frac{B_{2r} (-4)^r (1-4^r)}{(2r)!} x^{2r-1}+\cdots \qquad |x|<\frac{\pi}{2} | |||
</math><br/>where ''B<sub>k</sub>''=k<sup>th</sup> [[Bernoulli number]]. | |||
<br/><br/> | |||
===Inverse trigonometric functions=== | ===Inverse trigonometric functions=== | ||
:<math> | |||
\operatorname{tan^{-1}} x=x-\frac{x^3}{3}+\frac{x^5}{5}-\cdots+(-1)^{r}\frac{x^{2r+1}}{(2r+1)}+\cdots \qquad (-1 < x \le 1) | |||
</math><br/><br/> | |||
===Hyperbolic functions=== | ===Hyperbolic functions=== | ||
:<math> | |||
\sinh x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots+\frac{x^{2r+1}}{(2r+1)!}+\cdots \qquad \forall x | |||
</math><br/><br/> | |||
:<math> | |||
\cosh x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots+\frac{x^{2r}}{(2r)!}+\cdots \qquad \forall x | |||
</math><br/><br/> | |||
===Inverse hyperbolic functions=== | ===Inverse hyperbolic functions=== | ||
:<math> | |||
\operatorname{tanh^{-1}} x=x+\frac{x^3}{3}+\frac{x^5}{5}+\cdots+\frac{x^{2r+1}}{(2r+1)}+\cdots \qquad (-1 < x \le 1) | |||
</math><br/><br/> | |||
==Calculation of Taylor series for more complicated functions== | |||
[[Category:Suggestion Bot Tag]] | |||
[[Category: | |||
Latest revision as of 12:00, 25 October 2024
A Taylor series is an infinite sum of polynomial terms to approximate a function in the region about a certain point . This is only possible if the function is behaving analytically in this neighbourhood. Such series about the point are known as Maclaurin series, after Scottish mathematician Colin Maclaurin. They work by ensuring that the approximate series matches up to the nth derivative of the function being approximated when it is approximated by a polynomial of degree .
Proof
See Taylor's theorem
Series
General formula
An intuitive explanation of the Taylor series is that, in order to approximate the value of , as a first approximation we use the value at another point , i.e. . If and are close together and varies only slowly, this can be a good approximation. Then we refine the approximation step by step. The derivative of is used to calculate approximately how much would be expected to change between and , and this amount is added as a correction. But we assume we only know the derivative of at , and the derivative may change between the two numbers, so another correction is needed, involving the second derivative which is a measure of how much the first derivative changes. So it continues, adding corrections to corrections, and in the limit, if it converges then it converges to the actual value of even if and are far apart.
where is the first derivative of the function , and is the second derivative, and so on. Most practically used smooth functions satisfy this formula but not all of them. The smooth function have all derivatives equal to zero but the function itself is not equal to zero. In order to prove Taylor formula for particular functions, mathematicians reduce the problem to proving Taylor formula for basic functions using a variety of theorems. Taylor formula for basic functions can be proved directly by estimating their derivatives.
Convergence of the Taylor series and examples
Region of convergence of the Taylor series is always circle. This circle is centered at the point of expansion. Radius of this circle is equal to the distance from this point to the closest singulatiry. Within the circle of convergence, the Taylor series can be used to make the polynomial approximation of holomorphic functions, just truncating the series.
f(z)=1/z
The simple function, which is not polynomoal, is This function is shown in the left hand side of the figure in the complex plane with lines of constant and constant . The polynomial approximation of this function can be obtained truncating the Taylor series; for example, taking 21 terms of the Taylor series developed at gives the approximation
This function is shown in the right hand side of the figure. In the central part of the circle of convergence, the truncated Taylor series approximate the function.
Below, more example of Taylor series of various functions are suggested.
Exponential & Logarithmic functions
Trigonometric functions
where Bk=kth Bernoulli number.