Law of cosines: Difference between revisions
Jump to navigation
Jump to search

imported>Michael Underwood No edit summary |
mNo edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | |||
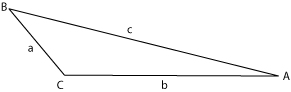
[[Image:Triangle.jpg|thumb|frame|Figure 1: A generic triangle with sides of length <math>a</math>, <math>b</math>, and <math>c</math> opposite the angles <math>A</math>, <math>B</math>, and <math>C</math>.]] | |||
In [[geometry]] the '''law of cosines''' is a useful identity for determining an angle or the length of one side of a triangle when given either two angles and three lengths or three angles and two lengths. When dealing with a right triangle, the law of cosines reduces to the [[Pythagorean theorem]] because of the fact that cos(90°)=0. To determine the areas of triangles, see the [[law of sines]]. The law of cosines can be stated as | In [[geometry]] the '''law of cosines''' is a useful identity for determining an angle or the length of one side of a triangle when given either two angles and three lengths or three angles and two lengths. When dealing with a right triangle, the law of cosines reduces to the [[Pythagorean theorem]] because of the fact that cos(90°)=0. To determine the areas of triangles, see the [[law of sines]]. The law of cosines can be stated as | ||
:<math> c^2 = \left(a^2 + b^2\right) - 2ab\cos(C) </math> | :<math> c^2 = \left(a^2 + b^2\right) - 2ab\cos(C) </math> | ||
where <math>a</math>, <math>b</math>, and <math>c</math> are the lengths of the sides of the triangle opposite to angles <math>A</math>, <math>B</math>, and <math>C</math>, respectively (see | where <math>a</math>, <math>b</math>, and <math>c</math> are the lengths of the sides of the triangle opposite to angles <math>A</math>, <math>B</math>, and <math>C</math>, respectively (see Figure 1).[[Category:Suggestion Bot Tag]] | ||
[[Category: | |||
Latest revision as of 12:00, 10 September 2024
In geometry the law of cosines is a useful identity for determining an angle or the length of one side of a triangle when given either two angles and three lengths or three angles and two lengths. When dealing with a right triangle, the law of cosines reduces to the Pythagorean theorem because of the fact that cos(90°)=0. To determine the areas of triangles, see the law of sines. The law of cosines can be stated as
where , , and are the lengths of the sides of the triangle opposite to angles , , and , respectively (see Figure 1).