Rocket engine: Difference between revisions
imported>Milton Beychok m (Added a space.) |
mNo edit summary |
||
| (14 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
{{seealso|Jet engine}} | |||
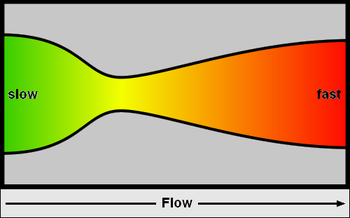
{{Image|De Laval nozzle.png|right|350px|Figure 1: Showing the flow velocity of the exhaust gas (from the propellant combustion) increasing from slow (green) to fast (red) in a de Laval nozzle as used in rocket engines.}} | |||
A '''rocket engine''', also called '''rocket motor''', actually propels a rocket-propelled | A '''rocket engine''', also called '''rocket motor''', actually propels a rocket-propelled guided missile or [[unguided rocket]]. The most general definition of such a propulsion system simply requires that it be independent of atmosphere, and propels a vehicle by the reaction to an action that releases energy in the opposite direction, one can consider even more exotica, such as ion generator propulsion. In general terms, two factors characterize the efficiency of a reaction-based propulsion system: the specific impulse (energy of the emitted particles), as described in a section below, and the mass of the system that produces the particles. With conventional rockets, the relationship with these factors change constantly, because as propellants are turned into exhaust, the mass of the propulsion system decreases; the implications of a changing mass ratio are a matter of overall vehicle design and exterior ballistics, and beyond the scope of this article. | ||
The most common forms, however, use chemical reactions to generate hot, fast-moving gases that are directed through an exhaust nozzle, and, as a reaction to the action of the moving gases, the engine develops thrust in the opposite direction to the exhaust gas flow. In these reactions, the reactants may be a single solid, a single liquid, or multiple liquid. As opposed to a gun, there is gas generation for seconds or even minutes. | The most common forms, however, use chemical reactions to generate hot, fast-moving gases that are directed through an exhaust nozzle, and, as a reaction to the action of the moving gases, the engine develops thrust in the opposite direction to the exhaust gas flow. In these reactions, the reactants may be a single solid, a single liquid, or multiple liquid. As opposed to a gun, there is gas generation for seconds or even minutes. | ||
==Ancestors of modern rockets== | |||
Rocket engines can be dated back to the invention of the [[aeolipile]] before the first century AD. This device used steam power directed through two nozzles so as to cause a sphere to spin rapidly on its axis. So far as is known, it was not used for supplying mechanical power, and the potential practical applications of this invention were not recognized. It was simply considered a curiosity. | |||
Jet propulsion only literally and figuratively took off with the invention of the [[rocket]] by the Chinese in the 13th century. Rocket exhaust was initially used in a modest way for [[fireworks]] but gradually progressed to propel formidable weaponry; and there the technology stalled for hundreds of years. | |||
[[Archytas]], the founder of mathematical mechanics, as described in the writings of Aulus Gellius five centuries after him, was reputed to have designed and built the first artificial, self-propelled flying device. This device was a bird-shaped model propelled by a jet of what was probably steam, said to have actually flown some 200 meters. | |||
In [[Ottoman Turkey]] in 1633 [[Lagari Hasan Çelebi]] took off with what was described to be a cone-shaped rocket and then glided with wings into a successful landing, winning a position in the [[Ottoman Empire|Ottoman]] army. However, this was essentially a stunt. The problem was that rockets are simply too inefficient at low speeds to be useful for general aviation. | |||
==Performance parameters== | ==Performance parameters== | ||
At the most elementary level, the more gas a rocket engine pushes through its nozzle, and the longer the time period for which it does so, the farther and faster the rocket will fly. | At the most elementary level, the more gas a rocket engine pushes through its nozzle, and the longer the time period for which it does so, the farther and faster the rocket will fly. | ||
===Velocity of gases exiting the rocket engine nozzle exhaust=== | ====Velocity of gases exiting the rocket engine nozzle exhaust==== | ||
The purpose of a propelling nozzle in a rocket engine is to expand and accelerate the [[combustion]] product gases from burning [[propellant]]s so that the gases are exhausted from the nozzle exit at [[supersonic]] [[Velocity|velocities]]. Most usually, rocket propelling nozzles are of the [[De Laval nozzle|de Laval]] type as depicted in the adjacent Figure 1. | The purpose of a propelling nozzle in a rocket engine is to expand and accelerate the [[combustion]] product gases from burning [[propellant]]s so that the gases are exhausted from the nozzle exit at [[supersonic]] [[Velocity|velocities]]. Most usually, rocket propelling nozzles are of the [[De Laval nozzle|de Laval]] type as depicted in the adjacent Figure 1. | ||
| Line 17: | Line 27: | ||
* For simplicity, the combustion gas is assumed to be an [[ideal gas]]. | * For simplicity, the combustion gas is assumed to be an [[ideal gas]]. | ||
* The gas flow is isentropic (i.e., at constant [[entropy (thermodynamics)|entropy]]), [[ | * The gas flow is isentropic (i.e., at constant [[entropy (thermodynamics)|entropy]]), [[Friction (science)|frictionless]], and [[adiabatic]] (i.e., there is little or no [[heat]] gained or lost) | ||
* The gas flow is constant (i.e., steady) during the period of the propellant burn. | * The gas flow is constant (i.e., steady) during the period of the propellant burn. | ||
* The gas flow is along a straight line from gas inlet to exhaust gas exit (i.e., along the nozzle's axis of symmetry) | * The gas flow is along a straight line from gas inlet to exhaust gas exit (i.e., along the nozzle's axis of symmetry) | ||
* The gas flow behavior is that of a [[compressible fluid]] (i.e., gas at high velocity). | * The gas flow behavior is that of a [[compressible fluid]] (i.e., gas at high velocity). | ||
As the combustion gas enters the rocket nozzle, it is traveling at [[subsonic]] velocities. As the throat contracts down the gas is forced to accelerate by the | As the combustion gas enters the rocket nozzle, it is traveling at [[subsonic]] velocities. As the throat contracts down the gas is forced to accelerate by the venturi effect until at the nozzle throat, where the cross-sectional area is the smallest, the linear velocity becomes sonic (i.e., attains the [[speed of sound]]). From the throat the cross-sectional area then increases, the gas expands and the linear velocity becomes progressively more supersonic. | ||
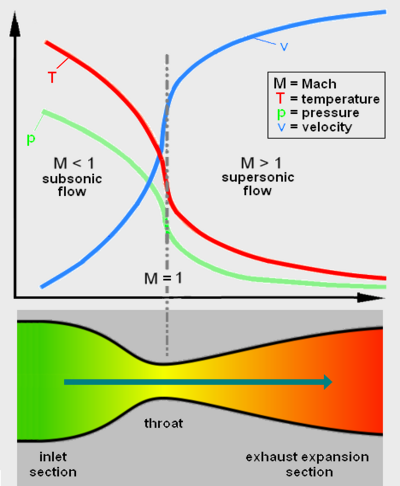
The linear velocity of the exiting exhaust gases can be calculated using the following equation:<ref name=Braeuning>[http://www.braeunig.us/space/propuls.htm#intro Robert Braeuning's Equation | {{Image|De Laval nozzle 2.png|right|400px|Fig. 2: Diagram of a de Laval nozzle, showing flow velocity (v) increasing in the direction of flow, with decreases in temperature (t) and pressure (p). The Mach number (M) increases from subsonic, to sonic at the throat, and then to supersonic.}} | ||
The linear velocity of the exiting exhaust gases can be calculated using the following equation:<ref name=Nakka>[http://www.nakka-rocketry.net/th_nozz.html Richard Nakka's Equation 12]</ref><ref name=Braeuning>[http://www.braeunig.us/space/propuls.htm#intro Robert Braeuning's Equation 1.22]</ref><ref>{{cite book|author=Sutton, George P.|title=Rocket Propulsion Elements: An Introduction to the Engineering of Rockets|edition=6th Edition|publisher=Wiley-Interscience|year=1992|isbn=0-471-52938-9|pages=page 636}}</ref> | |||
:<math> | :<math>v_e = \sqrt{\;\frac{T\;R}{M}\cdot\frac{2\;k}{k-1}\cdot\bigg[ 1-(p_e/p)^{(k-1)/k}\bigg]} </math> | ||
:where: | :where: | ||
:''''' | :'''''v<sub>e</sub>''''' = Exhaust velocity at nozzle exit, m/s<br/> | ||
:  '''''T''''' = absolute [[temperature]] of inlet gas, K | :  '''''T''''' = absolute [[temperature]] of inlet gas, K | ||
: '''''M''''' = the gas [[molecular mass]], kg/kmol (also known as the molecular weight) | : '''''R''''' = [[gas constant|Universal gas law constant]] = 8314.5 J/(kmol·K) | ||
: '''''M''''' = the gas [[molecular mass]], kg/kmol (also known as the molecular | |||
: weight) | |||
: '''''k''''' = '''''c<sub>p</sub>'''''/'''''c<sub>v</sub>''''' = [[Specific heat ratio|isentropic expansion factor]] | : '''''k''''' = '''''c<sub>p</sub>'''''/'''''c<sub>v</sub>''''' = [[Specific heat ratio|isentropic expansion factor]] | ||
:'''''c<sub>p</sub>''''' = [[specific heat]] of the gas at constant [[pressure]] | :'''''c<sub>p</sub>''''' = [[specific heat]] of the gas at constant [[pressure]] | ||
| Line 38: | Line 51: | ||
: '''''p''''' = absolute pressure of inlet combustion gas, Pa | : '''''p''''' = absolute pressure of inlet combustion gas, Pa | ||
Some typical values of the exhaust gas velocity ''''' | Some typical values of the exhaust gas velocity '''''v<sub>e</sub>''''' for rocket engines burning various propellants are: | ||
* 1.7 to 2.9 [[Kilometre|km]]/s (3,800 to 6,500 [[U.S. customary units|mi]]/h) for liquid [[monopropellant]]s | * 1.7 to 2.9 [[Kilometre|km]]/s (3,800 to 6,500 [[U.S. customary units|mi]]/h) for liquid [[monopropellant]]s | ||
| Line 44: | Line 57: | ||
* 2.1 to 3.2 km/s (4700 to 7,200 mi/h) for [[solid rocket|solid propellant]]s | * 2.1 to 3.2 km/s (4700 to 7,200 mi/h) for [[solid rocket|solid propellant]]s | ||
As a note of interest, ''''' | As a note of interest, '''''v<sub>e</sub>''''' is sometimes referred to as the ''ideal exhaust gas velocity'' because it based on the assumption that the exhaust gas behaves as an ideal gas. | ||
As an example calculation using the above equation, assume that the propellant combustion gases are: at an absolute pressure entering the nozzle of '''''p''''' = 7.0 MPa and exit the rocket exhaust at an absolute pressure of '''''p<sub>e</sub>''''' = 0.1 MPa; at an absolute temperature of '''''T''''' = 3500 K; with an isentropic expansion factor of '''''k''''' = 1.22 and a molecular mass of '''''M''''' = 22 kg/kmol. Using those values in the above equation yields an exhaust velocity '''''v<sub>e</sub>''''' = 2802 m/s or 2.80 km/s which is consistent with above typical values. | |||
The technical literature can be very confusing because many authors fail to explain whether they are using the universal gas law constant ''R'' which applies to any ideal gas or whether they are using the gas law constant '''''R'''''<sub>s</sub> which only applies to a specific individual gas. The relationship between the two constants is '''''R'''''<sub>s</sub> = '''''R'''''/'''''M'''''. | |||
====Rocket thrust and specific impulse==== | |||
Thrust is the [[force]] which moves a rocket through the air, and through space. Thrust is generated by the [[spacecraft propulsion|propulsion]] system of the rocket through the application of Newton's third law of motion: "For every action there is an equal and opposite reaction". A gas or working fluid is accelerated out the rear of the rocket engine nozzle and the rocket is accelerated in the opposite direction. The thrust of a rocket engine nozzle can be defined as:<ref name=Nakka/><ref name=Braeuning/><ref name=NASAThrust>[http://exploration.grc.nasa.gov/education/rocket/rockth.html NASA: Rocket thrust]</ref><ref name=NASASummary>[http://exploration.grc.nasa.gov/education/rocket/rktthsum.html NASA: Rocket thrust summary]</ref> | |||
=== | :{| border="0" cellpadding="2" | ||
|- | |||
!align=right|<math>F</math> | |||
|align=left|<math>=\dot{m}\,v_e + (p_e - p_o)\,A_e</math> | |||
|- | |||
!align=right| | |||
|align=left|<math>=\dot{m}\,\bigg[v_e + \bigg(\frac{p_e - p_o}{\dot{m}}\bigg)A_e\bigg]</math> | |||
|- | |||
!align=right| | |||
|align=left|<math>=\dot{m}\,v_{eq}</math> | |||
|} | |||
The specific impulse, <math>I_{sp}</math>, is the ratio of the amount of thrust produced to the weight flow of the [[propellant]]s. It is a measure of the fuel efficiency of a rocket engine. It can be obtained from:<ref name=NASAIsp>[http://exploration.grc.nasa.gov/education/rocket/specimp.html NASA:Rocket specific impulse]</ref> | |||
:<math>F = \dot {m} | :<math>I_{sp} =\, \frac{F}{\dot{m}\,g_o}\,=\, \frac{\dot{m}\,v_{eq}}{\dot{m}\,g_o}\,=\,\frac{v_{eq}}{g_o}</math> | ||
:{| border="0" cellpadding="2" | |||
|- | |||
|align=right|where: | |||
| | |||
|- | |||
!align=right|<math>F</math> | |||
|align=left|= rocket engine thrust, N | |||
|- | |||
!align=right|<math>\dot{m}</math> | |||
|align=left|= mass flow rate of exhaust gas, kg/s | |||
|- | |||
!align=right|<math>v_e</math> | |||
|align=left|= exhaust gas velocity at nozzle exit, m/s | |||
|- | |||
!align=right|<math>p_e</math> | |||
|align=left|= exhaust gas pressure at nozzle exit, Pa | |||
|- | |||
!align=right|<math>p_o</math> | |||
|align=left|= external ambient pressure, Pa (also known as free stream pressure) | |||
|- | |||
!align=right|<math>A_e</math> | |||
|align=left|= cross-sectional area of nozzle exhaust exit, m² | |||
|- | |||
!align=right|<math>v_eq</math> | |||
|align=left|= equivalent (or effective) exhaust gas velocity at nozzle exit, m/s | |||
|- | |||
!align=right|<math>I_{sp}</math> | |||
|align=left|= specific impulse, s | |||
|- | |||
!align=right|<math>g_o</math> | |||
|align=left|= Gravitational acceleration at sea level on Earth = 9.807 m/s² | |||
|} | |||
In certain cases, where <math>p_e</math> equals <math>p_o</math>, then: | |||
:<math>I_{sp} =\frac{F}{\dot{m}\,g_o}=\frac{\dot{m}\,v_{e}}{\dot{m}\,g_o}=\frac{v_{e}}{g_o}</math> | |||
As a quick but rough approximation in those cases, the specific impulse is the exhaust velocity divided by ten. | |||
==Throttling== | |||
Rockets can be throttled by controlling the propellant combustion rate '''''ṁ''''' (usually measured in kg/s or lb/s). In liquid and hybrid <ref>'''Note:''' Hybrid fueled rockets use solid propellant plus liquid or gaseous propellant.</ref> fueled rockets, the propellant flow entering the chamber is controlled using valves. In solid fueled rockets, it is controlled by using shaped propellant grains that will vary their surface area over the course of the burn; hence, solid fueled rockets cannot be controlled in real-time. | |||
Rockets can usually be throttled down to an exit pressure of about one-third of ambient pressure (often limited by flow separation in nozzles) and up to a maximum limit determined only by the mechanical strength of the engine. | |||
: | |||
In practice, the degree to which rockets can be throttled varies greatly, but most rockets can be throttled by a factor of 2 without great difficulty; the typical limitation is combustion stability, as for example, injectors need a minimum pressure to avoid triggering damaging oscillations (chugging or combustion instabilities); but injectors can often be optimized and tested for wider ranges. | |||
==Solid fuel systems== | ==Solid fuel systems== | ||
| Line 87: | Line 135: | ||
Solids are stable in storage for an appreciable period of time. Their greatest disadvantage is that, other than some experimental devices, they burn until there is no more propellant, and the burning rate cannot be adjusted in real time. The highest-energy solid propellants do not produce as much energy as the highest-energy liquid propellants, but this is not a major restriction; all modern military rockets used for propulsion, as opposed to directional adjustment, are solid-propellant. | Solids are stable in storage for an appreciable period of time. Their greatest disadvantage is that, other than some experimental devices, they burn until there is no more propellant, and the burning rate cannot be adjusted in real time. The highest-energy solid propellants do not produce as much energy as the highest-energy liquid propellants, but this is not a major restriction; all modern military rockets used for propulsion, as opposed to directional adjustment, are solid-propellant. | ||
The solid fuel boosters of the [[Space Shuttle]], for example, use [[ammonium perchlorate]] oxidizer, aluminium powder fuel, an iron oxide catalyst, and a rubberized binder. | |||
==Liquid fuel systems== | ==Liquid fuel systems== | ||
| Line 98: | Line 148: | ||
At a minimum, a liquid fuel system has propellant storage, a means of transferring the propellant(s) to the combustion chamber, one or more combustion chambers, and one or more subsystems to control the release of the products of combustion. There have been exotic variants, such as pumping fluid. to be used as reaction mass, but energized not by a chemical reaction but by heat generated from controlled nuclear fission.<ref name=NukeRocketSci>[https://engineering.purdue.edu/AAE/Academics/Courses/aae539/2008/nuke_seminar.pdf Rocket Propulsion Fundamentals & Nuclear Thermal Propulsion] Steve Heister, School of Aeronautics and Astronautics, Purdue University, pp. 9-17</ref> | At a minimum, a liquid fuel system has propellant storage, a means of transferring the propellant(s) to the combustion chamber, one or more combustion chambers, and one or more subsystems to control the release of the products of combustion. There have been exotic variants, such as pumping fluid. to be used as reaction mass, but energized not by a chemical reaction but by heat generated from controlled nuclear fission.<ref name=NukeRocketSci>[https://engineering.purdue.edu/AAE/Academics/Courses/aae539/2008/nuke_seminar.pdf Rocket Propulsion Fundamentals & Nuclear Thermal Propulsion] Steve Heister, School of Aeronautics and Astronautics, Purdue University, pp. 9-17</ref> | ||
===Storage=== | ====Storage==== | ||
Cryogenic propellants need highly specialized, heavily insulated tanks, pumps and piping. For relatively small volumes such as the WWII V-2, a truck could deliver it, but, for modern large rockets that use cryogenic fuel or oxidizer, storage, and sometimes production facilities, need to be near the launch site. | Cryogenic propellants need highly specialized, heavily insulated tanks, pumps and piping. For relatively small volumes such as the WWII V-2, a truck could deliver it, but, for modern large rockets that use cryogenic fuel or oxidizer, storage, and sometimes production facilities, need to be near the launch site. | ||
Since these fluids are gases at room temperature, any tank containing them must have pressure relief valves to deal with the constant production of gas. Typically, they can be held inside the rocket internal tanks for no more than tens of hours, due both to outgassing and the effects, on mechanical components, of the supercold liquids. | Since these fluids are gases at room temperature, any tank containing them must have pressure relief valves to deal with the constant production of gas. Typically, they can be held inside the rocket internal tanks for no more than tens of hours, due both to outgassing and the effects, on mechanical components, of the supercold liquids. | ||
===Transfer inside the rocket body=== | |||
====Transfer inside the rocket body==== | |||
While some transfer systems rely on pressurized tanks, perhaps with a variable-flow valve, most high-performance transfer requires [[pump]]s. Pumps need a source of power, which is usually separate from the main reaction. For example, the [[V-2]] pumps used concentrated [[hydrogen peroxide]] breakdown to produce a gas stream that ran pumps for the [[liquid oxygen]] oxidizer and [[ethanol]] fuel. | While some transfer systems rely on pressurized tanks, perhaps with a variable-flow valve, most high-performance transfer requires [[pump]]s. Pumps need a source of power, which is usually separate from the main reaction. For example, the [[V-2]] pumps used concentrated [[hydrogen peroxide]] breakdown to produce a gas stream that ran pumps for the [[liquid oxygen]] oxidizer and [[ethanol]] fuel. | ||
===Combustion=== | |||
====Combustion==== | |||
Especially with cryogenic propellants, liquids can be piped around the outside of combustion and exhaust components, both to cool the components and preheat the propellants. This is called regenerative cooling. | Especially with cryogenic propellants, liquids can be piped around the outside of combustion and exhaust components, both to cool the components and preheat the propellants. This is called regenerative cooling. | ||
==References== | ==References== | ||
{{reflist|2}} | {{reflist|2}}[[Category:Suggestion Bot Tag]] | ||
Latest revision as of 07:00, 13 October 2024
- See also: Jet engine
A rocket engine, also called rocket motor, actually propels a rocket-propelled guided missile or unguided rocket. The most general definition of such a propulsion system simply requires that it be independent of atmosphere, and propels a vehicle by the reaction to an action that releases energy in the opposite direction, one can consider even more exotica, such as ion generator propulsion. In general terms, two factors characterize the efficiency of a reaction-based propulsion system: the specific impulse (energy of the emitted particles), as described in a section below, and the mass of the system that produces the particles. With conventional rockets, the relationship with these factors change constantly, because as propellants are turned into exhaust, the mass of the propulsion system decreases; the implications of a changing mass ratio are a matter of overall vehicle design and exterior ballistics, and beyond the scope of this article.
The most common forms, however, use chemical reactions to generate hot, fast-moving gases that are directed through an exhaust nozzle, and, as a reaction to the action of the moving gases, the engine develops thrust in the opposite direction to the exhaust gas flow. In these reactions, the reactants may be a single solid, a single liquid, or multiple liquid. As opposed to a gun, there is gas generation for seconds or even minutes.
Ancestors of modern rockets
Rocket engines can be dated back to the invention of the aeolipile before the first century AD. This device used steam power directed through two nozzles so as to cause a sphere to spin rapidly on its axis. So far as is known, it was not used for supplying mechanical power, and the potential practical applications of this invention were not recognized. It was simply considered a curiosity.
Jet propulsion only literally and figuratively took off with the invention of the rocket by the Chinese in the 13th century. Rocket exhaust was initially used in a modest way for fireworks but gradually progressed to propel formidable weaponry; and there the technology stalled for hundreds of years.
Archytas, the founder of mathematical mechanics, as described in the writings of Aulus Gellius five centuries after him, was reputed to have designed and built the first artificial, self-propelled flying device. This device was a bird-shaped model propelled by a jet of what was probably steam, said to have actually flown some 200 meters.
In Ottoman Turkey in 1633 Lagari Hasan Çelebi took off with what was described to be a cone-shaped rocket and then glided with wings into a successful landing, winning a position in the Ottoman army. However, this was essentially a stunt. The problem was that rockets are simply too inefficient at low speeds to be useful for general aviation.
Performance parameters
At the most elementary level, the more gas a rocket engine pushes through its nozzle, and the longer the time period for which it does so, the farther and faster the rocket will fly.
Velocity of gases exiting the rocket engine nozzle exhaust
The purpose of a propelling nozzle in a rocket engine is to expand and accelerate the combustion product gases from burning propellants so that the gases are exhausted from the nozzle exit at supersonic velocities. Most usually, rocket propelling nozzles are of the de Laval type as depicted in the adjacent Figure 1.
The analysis of gas flow exit velocity from de Laval nozzles involves a number of concepts and assumptions:
- For simplicity, the combustion gas is assumed to be an ideal gas.
- The gas flow is isentropic (i.e., at constant entropy), frictionless, and adiabatic (i.e., there is little or no heat gained or lost)
- The gas flow is constant (i.e., steady) during the period of the propellant burn.
- The gas flow is along a straight line from gas inlet to exhaust gas exit (i.e., along the nozzle's axis of symmetry)
- The gas flow behavior is that of a compressible fluid (i.e., gas at high velocity).
As the combustion gas enters the rocket nozzle, it is traveling at subsonic velocities. As the throat contracts down the gas is forced to accelerate by the venturi effect until at the nozzle throat, where the cross-sectional area is the smallest, the linear velocity becomes sonic (i.e., attains the speed of sound). From the throat the cross-sectional area then increases, the gas expands and the linear velocity becomes progressively more supersonic.
The linear velocity of the exiting exhaust gases can be calculated using the following equation:[1][2][3]
- where:
- ve = Exhaust velocity at nozzle exit, m/s
- T = absolute temperature of inlet gas, K
- R = Universal gas law constant = 8314.5 J/(kmol·K)
- M = the gas molecular mass, kg/kmol (also known as the molecular
- weight)
- k = cp/cv = isentropic expansion factor
- cp = specific heat of the gas at constant pressure
- cp = specific heat of the gas at constant volume
- pe = absolute pressure of exhaust gas at nozzle exit, Pa
- p = absolute pressure of inlet combustion gas, Pa
Some typical values of the exhaust gas velocity ve for rocket engines burning various propellants are:
- 1.7 to 2.9 km/s (3,800 to 6,500 mi/h) for liquid monopropellants
- 2.9 to 4.5 km/s (6,500 to 10,100 mi/h) for liquid bipropellants
- 2.1 to 3.2 km/s (4700 to 7,200 mi/h) for solid propellants
As a note of interest, ve is sometimes referred to as the ideal exhaust gas velocity because it based on the assumption that the exhaust gas behaves as an ideal gas.
As an example calculation using the above equation, assume that the propellant combustion gases are: at an absolute pressure entering the nozzle of p = 7.0 MPa and exit the rocket exhaust at an absolute pressure of pe = 0.1 MPa; at an absolute temperature of T = 3500 K; with an isentropic expansion factor of k = 1.22 and a molecular mass of M = 22 kg/kmol. Using those values in the above equation yields an exhaust velocity ve = 2802 m/s or 2.80 km/s which is consistent with above typical values.
The technical literature can be very confusing because many authors fail to explain whether they are using the universal gas law constant R which applies to any ideal gas or whether they are using the gas law constant Rs which only applies to a specific individual gas. The relationship between the two constants is Rs = R/M.
Rocket thrust and specific impulse
Thrust is the force which moves a rocket through the air, and through space. Thrust is generated by the propulsion system of the rocket through the application of Newton's third law of motion: "For every action there is an equal and opposite reaction". A gas or working fluid is accelerated out the rear of the rocket engine nozzle and the rocket is accelerated in the opposite direction. The thrust of a rocket engine nozzle can be defined as:[1][2][4][5]
The specific impulse, , is the ratio of the amount of thrust produced to the weight flow of the propellants. It is a measure of the fuel efficiency of a rocket engine. It can be obtained from:[6]
where: = rocket engine thrust, N = mass flow rate of exhaust gas, kg/s = exhaust gas velocity at nozzle exit, m/s = exhaust gas pressure at nozzle exit, Pa = external ambient pressure, Pa (also known as free stream pressure) = cross-sectional area of nozzle exhaust exit, m² = equivalent (or effective) exhaust gas velocity at nozzle exit, m/s = specific impulse, s = Gravitational acceleration at sea level on Earth = 9.807 m/s²
In certain cases, where equals , then:
As a quick but rough approximation in those cases, the specific impulse is the exhaust velocity divided by ten.
Throttling
Rockets can be throttled by controlling the propellant combustion rate ṁ (usually measured in kg/s or lb/s). In liquid and hybrid [7] fueled rockets, the propellant flow entering the chamber is controlled using valves. In solid fueled rockets, it is controlled by using shaped propellant grains that will vary their surface area over the course of the burn; hence, solid fueled rockets cannot be controlled in real-time.
Rockets can usually be throttled down to an exit pressure of about one-third of ambient pressure (often limited by flow separation in nozzles) and up to a maximum limit determined only by the mechanical strength of the engine.
In practice, the degree to which rockets can be throttled varies greatly, but most rockets can be throttled by a factor of 2 without great difficulty; the typical limitation is combustion stability, as for example, injectors need a minimum pressure to avoid triggering damaging oscillations (chugging or combustion instabilities); but injectors can often be optimized and tested for wider ranges.
Solid fuel systems
Solid propellants allow much simpler construction, as they do not need pumps to move them into a combustion chamber. Indeed, black gunpowder, as the first solid propellant, was introduced in the 13th century.
Solids are stable in storage for an appreciable period of time. Their greatest disadvantage is that, other than some experimental devices, they burn until there is no more propellant, and the burning rate cannot be adjusted in real time. The highest-energy solid propellants do not produce as much energy as the highest-energy liquid propellants, but this is not a major restriction; all modern military rockets used for propulsion, as opposed to directional adjustment, are solid-propellant.
The solid fuel boosters of the Space Shuttle, for example, use ammonium perchlorate oxidizer, aluminium powder fuel, an iron oxide catalyst, and a rubberized binder.
Liquid fuel systems
First demonstrated in 1926, liquid engines offer much more control over thrust, and generally higher energy than solid propellants.[8] They usually usually mix two liquids, a fuel and an oxidizer, although there are monopropellants. Every fuel-oxidizer system has advantages and disadvantages. The highest-energy mixes, such as hydrogen and oxygen, use cryogenic (intensely cold) liquids, which are difficult to store and pump. Cryogenic systems also need an ignition system.
Storable liquid propellants, such as a hydrazine-based compound and red fuming nitric acid or a relative, can be held at normal temperatures, but tend to be very toxic and corrosive. The combinations are often hypergolic, igniting on contact.
At a minimum, a liquid fuel system has propellant storage, a means of transferring the propellant(s) to the combustion chamber, one or more combustion chambers, and one or more subsystems to control the release of the products of combustion. There have been exotic variants, such as pumping fluid. to be used as reaction mass, but energized not by a chemical reaction but by heat generated from controlled nuclear fission.[9]
Storage
Cryogenic propellants need highly specialized, heavily insulated tanks, pumps and piping. For relatively small volumes such as the WWII V-2, a truck could deliver it, but, for modern large rockets that use cryogenic fuel or oxidizer, storage, and sometimes production facilities, need to be near the launch site.
Since these fluids are gases at room temperature, any tank containing them must have pressure relief valves to deal with the constant production of gas. Typically, they can be held inside the rocket internal tanks for no more than tens of hours, due both to outgassing and the effects, on mechanical components, of the supercold liquids.
Transfer inside the rocket body
While some transfer systems rely on pressurized tanks, perhaps with a variable-flow valve, most high-performance transfer requires pumps. Pumps need a source of power, which is usually separate from the main reaction. For example, the V-2 pumps used concentrated hydrogen peroxide breakdown to produce a gas stream that ran pumps for the liquid oxygen oxidizer and ethanol fuel.
Combustion
Especially with cryogenic propellants, liquids can be piped around the outside of combustion and exhaust components, both to cool the components and preheat the propellants. This is called regenerative cooling.
References
- ↑ 1.0 1.1 Richard Nakka's Equation 12
- ↑ 2.0 2.1 Robert Braeuning's Equation 1.22
- ↑ Sutton, George P. (1992). Rocket Propulsion Elements: An Introduction to the Engineering of Rockets, 6th Edition. Wiley-Interscience, page 636. ISBN 0-471-52938-9.
- ↑ NASA: Rocket thrust
- ↑ NASA: Rocket thrust summary
- ↑ NASA:Rocket specific impulse
- ↑ Note: Hybrid fueled rockets use solid propellant plus liquid or gaseous propellant.
- ↑ The First Liquid Fuel Rocket, Goddard Space Flight Center, National Aeronautics and Space Administration
- ↑ Rocket Propulsion Fundamentals & Nuclear Thermal Propulsion Steve Heister, School of Aeronautics and Astronautics, Purdue University, pp. 9-17
![{\displaystyle v_{e}={\sqrt {\;{\frac {T\;R}{M}}\cdot {\frac {2\;k}{k-1}}\cdot {\bigg [}1-(p_{e}/p)^{(k-1)/k}{\bigg ]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4752afcd55c194ba53acb3d0034d0eb203e3e0fe)


![{\displaystyle ={\dot {m}}\,{\bigg [}v_{e}+{\bigg (}{\frac {p_{e}-p_{o}}{\dot {m}}}{\bigg )}A_{e}{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a909ce130c0af4fa0c06feb98feb1cffd034985)










