Logarithm: Difference between revisions
imported>Milton Beychok m (→Notational variants: Changed script style math expressions to regular math expressions for consistency with the rest of the article. Also, adjusted alignment of a math expression.) |
imported>Milton Beychok m (→Complex numbers and logarithms: Changed script style math expressions to regular math expressions for consistency. Also aligned some math expressions imbedded in the text.) |
||
| Line 85: | Line 85: | ||
:<math>e^{u + vi} = e^u(\cos(v) + i\sin(v)).\,</math> | :<math>e^{u + vi} = e^u(\cos(v) + i\sin(v)).\,</math> | ||
The sine and cosine functions are not [[one-to-one function|one-to-one]] and hence neither is this complex [[exponential function]]. Therefore it has no inverse function, as the concept of "function" is generally defined in the present day. However | The sine and cosine functions are not [[one-to-one function|one-to-one]] and hence neither is this complex [[exponential function]]. Therefore it has no inverse function, as the concept of "function" is generally defined in the present day. However, one may speak of the logarithm as being a [[multiple-valued function]] (strictly speaking, an oxymoronic term by current conventions). | ||
To find the logarithm of a complex number <math>a + bi</math>, it is convenient to express the number in polar coordinates <math>(r,\theta)</math> where <math> | To find the logarithm of a complex number <math>a + bi</math>, it is convenient to express the number in polar coordinates <math>(r,\theta)</math> where <font style="vertical-align:20%;"><math>r = \sqrt{a^2 + b^2}</math></font> and <math>\theta = \arctan(b/a)</math>. (Intuitively, <math>r</math> is the length of the line segment joining the number to the origin in the complex plane, and <math>\theta</math> is the angle that line segment makes with the <math>x</math>-axis). The equivalence of the two notations is given by | ||
:<math>a + bi = r(\cos(\theta) + i \sin(\theta)).\,</math> | :<math>a + bi = r(\cos(\theta) + i \sin(\theta)).\,</math> | ||
Let us define <font style="vertical-align:+5%;"><math>c + di</math></font> so that <math>\ln(a + bi) = c + di</math>. Using the formula for the exponential function above, | |||
:<math>a + bi = e^{c + di} = e^ce^{di} = e^c(\cos(d) + i \sin(d)).\,</math> | :<math>a + bi = e^{c + di} = e^ce^{di} = e^c(\cos(d) + i \sin(d)).\,</math> | ||
It can be seen from similarity with the above formula for polar coordinates that <math> | It can be seen from similarity with the above formula for polar coordinates that <font style="vertical-align:+10%;"><math>r = e^c</math></font> and <font style="vertical-align:+10%;"><math>d = \theta</math></font>. Therefore, | ||
:<math>\ln(a + bi) = c + di = \ln( r ) + i \theta = \ln(\sqrt{a^2 + b^2}) + i \arctan\left(\frac{b}{a}\right).\,</math> | :<math>\ln(a + bi) = c + di = \ln( r ) + i \theta = \ln(\sqrt{a^2 + b^2}) + i \arctan\left(\frac{b}{a}\right).\,</math> | ||
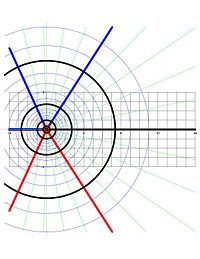
This is "multiple-valued" because the arctangent function is "multiple-valued". If <math>w</math> is a value of <math>ln(a + bi),</math> then <math>w + 2n\pi i</math> is also a value of the "function" for any integer <math>n</math>. A single-valued function can be obtained by, for example, restricting the values of the <math>arctan</math> function to <math>-\pi < \theta <= \pi</math>. | This is "multiple-valued" because the arctangent function is "multiple-valued". If <math>w</math> is a value of <math>ln(a + bi),</math> then <math>w + 2n\pi i</math> is also a value of the "function" for any integer <math>n</math>. A single-valued function can be obtained by, for example, restricting the values of the <font style="vertical-align:5%;"><math>arctan</math></font> function to <font style="vertical-align:+15%;"><math>-\pi < \theta <= \pi</math></font>. In this case, the complex logarithm function has a discontinuity along the negative <math>x</math>-axis (see figure). | ||
In this way, the domain of the logarithmic function can be extended to cover the entire complex plane except for the number zero, which has an undefined value — a singularity with the real part plunging towards minus infinity and the imaginary part spinning wildly like a compass at the north pole. | In this way, the domain of the logarithmic function can be extended to cover the entire complex plane except for the number zero, which has an undefined value — a singularity with the real part plunging towards minus infinity and the imaginary part spinning wildly like a compass at the north pole. | ||
Revision as of 18:38, 26 October 2008
Computing logarithms is the inverse of exponentiation, as subtraction is the inverse of addition and division is the inverse of multiplication. For example, since , then the base-7 logarithm of 343 is 3. In general, if , then where is called the base and is the logarithm. In other words, the logarithm is the exponential power to which the base must be raised to produce the number .
Logarithms show up in a variety of scientific formulas: for example, the number of bits required to represent the address of a particular location in computer memory is equal to the base-2 logarithm (rounded upwards) of the number of possible locations. Logarithms are also useful for representing large numbers in a more manageable form.
Logarithms of intermediate and fractional values
Because we use a base-10 number system, it is often convenient to use 10 as the base of the logarithm. It's easy to find the base-10 logarithm of a number such as 1000, because therefore (The value of the logarithmic function is the number that appeared as an exponent in the other equation.) But what is the logarithm of a number such as 43, or 0.001?
We know from the study of exponents that, for example, is and this then supplies a value for Values for many other numbers can be worked out similarly using cube roots and so on, and values for all real numbers can then be defined using limits. For example, is approximately equal to 1.63347. Multiplying a number by 10 appends a zero to the numeral and adds 1 to the base-10 logarithm, therefore is approximately 2.63347.
and it then follows that
or in general,
By a similar argument it can be established that for any base and therefore that
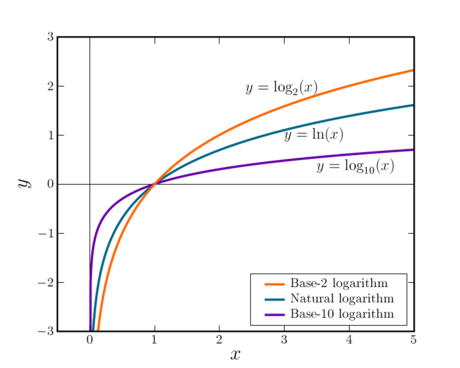
Thus, logarithms of numbers between 0 and 1 are negative numbers, the logarithm of 1 is 0, and logarithms of numbers greater than 1 are positive real numbers as seen in the image below.
Shape of the logarithm function
Consider the function where b is a real-number base greater than 1 of the logarithm. Since any positive real number raised to the exponent zero is 1, the logarithm of 1 is zero. To the right of 1 on the x-axis, the function continually increases, but increases more and more slowly as heads towards infinity. Between 1 and 0, the logarithmic function has negative values, and asymptotically approaches minus infinity as approaches zero. For negative values of , there is no defined value of within the real numbers — but using complex numbers a value can be found, as will be discussed further below.
Manipulating logarithms
Suppose we know the logarithm of a number using one base , and we want to find the logarithm using a different base :
- ?
Suppose we know , and and we want to find . We need to look up the value of , and then by multiplying we can find the desired quantity:
This formula can be established using the definition of logarithms and the rule for multiplying exponents:
Substituting for b,
Therefore , the formula we wished to prove.
A useful formula for can be derived using the rule for adding exponents:
Therefore :
Other useful formulas include these identities:
Notational variants
When logarithms are used to measure physical values (e.g., when noise is measured in deciBels) it is common to use 10 as a base, and in these contexts, the notation means .
Mathematicians and physicists often find, however, that the transcendental number , also known as Euler's number, is more convenient as a base for a logarithmic function. The value of is approximately equal to 2.718281828459045. The logarithmic function with as a base is called the natural logarithm; it has the special property that its derivative is . The notation is often used for natural logarithms, but in mathematics it is just as common to use the notation and write logarithms to base 10 using the full notation .
Computer science adds a whole new wrinkle because, in some cases, it is most useful to consider logarithms to base 2, and this has led to a new notation which become common for logarithms to a base of 2. Finally, the notation is sometimes used for logarithms to base 2, but this is usage is less common.
Complex numbers and logarithms
The exponential function of an imaginary number is given as
Consequently if a and b are real numbers then
The sine and cosine functions are not one-to-one and hence neither is this complex exponential function. Therefore it has no inverse function, as the concept of "function" is generally defined in the present day. However, one may speak of the logarithm as being a multiple-valued function (strictly speaking, an oxymoronic term by current conventions).
To find the logarithm of a complex number , it is convenient to express the number in polar coordinates where and . (Intuitively, is the length of the line segment joining the number to the origin in the complex plane, and is the angle that line segment makes with the -axis). The equivalence of the two notations is given by
Let us define so that . Using the formula for the exponential function above,
It can be seen from similarity with the above formula for polar coordinates that and . Therefore,
This is "multiple-valued" because the arctangent function is "multiple-valued". If is a value of then is also a value of the "function" for any integer . A single-valued function can be obtained by, for example, restricting the values of the function to . In this case, the complex logarithm function has a discontinuity along the negative -axis (see figure).
In this way, the domain of the logarithmic function can be extended to cover the entire complex plane except for the number zero, which has an undefined value — a singularity with the real part plunging towards minus infinity and the imaginary part spinning wildly like a compass at the north pole.






































![{\displaystyle \log _{b}({\sqrt[{y}]{x}})={\frac {\log _{b}(x)}{y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbb5fcbb3fb6949b7a9549bd3d8cf128843f3cf3)