User:Milton Beychok/Sandbox

Gas stoichiometry is the quantitative relationship between the reactants and products in chemical reactions that produce gases. Gas stoichiometry applies when all of the gases involved in a chemical reaction (either reactants or products) may be assumed to be ideal, and the temperature and pressure of the gases are all known. Often, but not always, the reference conditions used for gas stoichiometric calculations are taken to be a temperature of 0 °C and an absolute pressure of 1 atm.

History

In 1792, the German chemist Jeremias Benjamin Richter first proposed the concept of the quantitative mass relationships that exist between the chemicals involved in chemical reactions:

In German: Die stöchyometrie (Stöchyometria) ist die Wissenschaft die quantitativen oder Massenverhältnisse zu messen, in welchen die chymischen Elemente gegen einander stehen." (In English: Stoichiometry is the science of measuring the quantitative proportions or mass ratios in which chemical elements stand to one another.)

He named this quantitative study of chemistry to be "stoichiometry", from two Greek words meaning to measure the magnitude of something that cannot be divided.

Richter's introduction of the term "stoichiometry" substantially predated the introduction of the atomic hypothesis in 1803 by the English eminent scientist John Dalton.

Example calculations

Gas stoichiometry calculations solve for the unknown volume or mass of gaseous products and/or reactants involved in chemical reactions by using, for the most part, the ideal gas law.

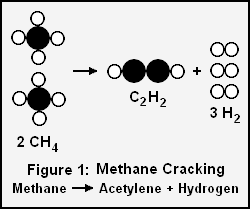
Acetylene and hydrogen produced by cracking methane

(PD) Diagram: Milton Beychok

For example, if we want to determine the volume of acetylene and hydrogen gases produced by cracking 100 grams of methane gas as per this chemical reaction:

2 CH₄ (g) → C₂H₂ (g) + 3H₂

2 moles of methane gas → 1 mole of acetylene gas + 3 moles of hydrogen gas

Determining the moles of methane (molar mass = 16.04 g/mol) equivalent to 100 grams :

$100\ {\mbox{g}}\,\cdot {\frac {1\ {\mbox{mole}}\ CH_{4}}{16.04\ {\mbox{g}}}}\,=\,6.234\ {\mbox{mole}}\ CH_{4}$

There is a 2 to 1 molar ratio of methane (CH₄) to product acetylene (C₂H₂) in the above cracking reaction, so 3.117 moles of acetylene will be formed.

The ideal gas law and the universal molar gas constant of R = 8.205745 × 10 ⁻⁵ m³ $\cdot$ atm $\cdot$ K ⁻¹$\cdot$ mol ⁻¹ can now be used to solve for the volume of acetylene formed at 0 °C (273.15 K) and 1 atmosphere:

$PV$	$=\,nRT$
$V$	$={\frac {nRT}{P}}={\frac {3.117\cdot 8.205745\cdot 10^{-5}\cdot 273.15}{1}}=0.06986\ {\mbox{m}}^{3}\ C_{2}H_{2}=69.86\ {\mbox{L}}\ C_{2}H_{2}$

The molar ratio of methane to product hydrogen (H₂) in the above cracking reaction is 1 to 1.5, so 9.351 moles of hydrogen will be formed. Again using the ideal gas law, the volume of hydrogen formed at 0 °C (273.15 K) and 1 atmosphere will be:

$V$	$={\frac {nRT}{P}}={\frac {9.351\cdot 8.205745\cdot 10^{-5}\cdot 273.15}{1}}=0.20959\ {\mbox{m}}^{3}\ H_{2}=209.59\ {\mbox{L}}\ H_{2}$

The molar mass of acetylene and the molar mass of hydrogen are 26.036 g/mol and 2.0158 g/mol respectively, the mass of acetylene formed is 26.036 × 3.117 = 81.15 g and the mass of hydrogen formed is 2.0158 × 9.351 = 18.85 g. The total mass of products is then 81.15 + 18.85 = 100.00 g which is equal to the mass of the reactant methane, and that satisfies the law of conservation of mass.

The parameters in the above equations are:

$P$	= absolute gas pressure, in atm
$V$	= gas volume, in m3
$n$	= number of moles, in mol
$T$	= absolute gas temperature, in K
$M$	= molar mass of gas, in g/mol
$R$	= 8.205745 × 10 −5 = universal molar gas constant, in m3 $\cdot$ atm $\cdot$ K −1$\cdot$ mol −1

Nitrogen and hydrogen needed for ammonia synthesis

(PD) Diagram: Milton Beychok

As another example, if we want to determine the amounts of nitrogen and hydrogen gases required to produce 5 kg of ammonia gas per this chemical reaction for the synthesis of ammonia:

N₂ + 3 H₂ → 2 NH₃

1 mole of nitrogen gas + 3 moles of hydrogen gas → 2 moles of ammonia gas

Determining the the moles of ammonia (molar mass = 17.03 g/mol) equivalent to 5 kilograms:

$5,000\ {\mbox{g}}\,\cdot {\frac {1\ {\mbox{mole}}\ NH_{3}}{17.03\ {\mbox{g}}}}\,=\,293.60\ {\mbox{mole}}\ NH_{3}$