Rotation matrix

In mathematics and physics a rotation matrix is synonymous with a 3×3 orthogonal matrix, which is a matrix R satisfying

$\mathbf {R} ^{\mathrm {T} }=\mathbf {R} ^{-1},$

where T stands for the transposed matrix and R⁻¹ is the inverse of R.

Connection of an orthogonal matrix to a rotation

In general a motion of a rigid body (which is equivalent to an angle and distance preserving transformation of affine space) can be described as a translation of the body followed by a rotation. By a translation all points of the rigid body are displaced, while under a rotation at least one point stays in place. Let the the fixed point be O. By Euler's theorem follows that then not only the point is fixed but also an axis—the rotation axis— through the fixed point. Write ${\hat {n}}$ for the unit vector along the rotation axis and φ for the angle over which the body is rotated, then the rotation operator on $\mathbb {R} ^{3}$ is written as ${\mathcal {R}}(\varphi ,{\hat {n}}).$

Erect three Cartesian coordinate axes with the origin in the fixed point O and take unit vectors ${\hat {e}}_{x},\;{\hat {e}}_{y},\;{\hat {e}}_{z}$ along the axes, then the 3×3 rotation matrix $\mathbf {R} (\varphi ,{\hat {n}})$ is defined by its elements $R_{ji}(\varphi ,{\hat {n}})$ :

${\mathcal {R}}(\varphi ,{\hat {n}})({\hat {e}}_{i})=\sum _{j=x,y,x}{\hat {e}}_{j}R_{ji}(\varphi ,{\hat {n}})\quad {\hbox{for}}\quad i=x,y,z.$

In a more condensed notation this equation can be written as

${\mathcal {R}}(\varphi ,{\hat {n}})\left({\hat {e}}_{x},\;{\hat {e}}_{y},\;{\hat {e}}_{z}\right)=\left({\hat {e}}_{x},\;{\hat {e}}_{y},\;{\hat {e}}_{z}\right)\;\mathbf {R} (\varphi ,{\hat {n}}).$

Given a basis of a linear space, the association between a linear map and its matrix is one-to-one.

Since a rotation ${\mathcal {R}}$ (for convenience sake the rotation axis and angle are suppressed in the notation) leaves all angles and distances invariant, for any pair of vectors ${\vec {a}}$ and ${\vec {b}}$ in $\mathbb {R} ^{3}$ the inner product is invariant, that is,

$\left({\mathcal {R}}({\vec {a}}),\;{\mathcal {R}}({\vec {b}})\right)=\left({\vec {a}},\;{\vec {b}}\right).$

A linear map with this property is called orthogonal. It is easily shown that a similar vector-matrix relation holds. First we define column vectors (stacked triplets of real numbers given in bold face):

${\vec {a}}=\left({\hat {e}}_{x},\;{\hat {e}}_{y},\;{\hat {e}}_{z}\right){\begin{pmatrix}a_{x}\\a_{y}\\a_{z}\end{pmatrix}}\;{\stackrel {\mathrm {def} }{=}}\;\left({\hat {e}}_{x},\;{\hat {e}}_{y},\;{\hat {e}}_{z}\right)\mathbf {a} \quad {\hbox{and}}\quad {\vec {b}}=\left({\hat {e}}_{x},\;{\hat {e}}_{y},\;{\hat {e}}_{z}\right){\begin{pmatrix}b_{x}\\b_{y}\\b_{z}\end{pmatrix}}\;{\stackrel {\mathrm {def} }{=}}\;\left({\hat {e}}_{x},\;{\hat {e}}_{y},\;{\hat {e}}_{z}\right)\mathbf {b}$

and observe that the inner product becomes by virtue of the orthonormality of the basis vectors

$\left({\vec {a}},\;{\vec {b}}\right)=\mathbf {a} ^{\mathrm {T} }\mathbf {b} \equiv \left(a_{x},\;a_{y},\;a_{z}\right){\begin{pmatrix}b_{x}\\b_{y}\\b_{z}\end{pmatrix}}\equiv a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}.$

The invariance of the inner product under the rotation operator ${\mathcal {R}}$ leads to

${\big (}\mathbf {R} \mathbf {a} {\big )}^{\mathrm {T} }\;\mathbf {R} \mathbf {b} =\mathbf {a} ^{\mathrm {T} }\mathbf {R} ^{\mathrm {T} }\;\mathbf {R} \mathbf {b}$

since this holds for any pair a and b it follows that a rotation matrix satisfies

$\mathbf {R} ^{\mathrm {T} }\mathbf {R} =\mathbf {E}$

where E is the 3×3 identity matrix. For finite-dimensional matrices one shows easily

$\mathbf {R} ^{\mathrm {T} }\mathbf {R} =\mathbf {E} \quad \Longleftrightarrow \quad \mathbf {R} \mathbf {R} ^{\mathrm {T} }=\mathbf {E} .$

A matrix with this property is called orthogonal. So, a rotation gives rise to a unique orthogonal matrix.

Conversely, consider an arbitrary point P in the body and let the vector ${\overrightarrow {OP}}$ connect the fixed point O with P. Expressing this vector with respect to a Cartesian frame in O gives the column vector p (three stacked real numbers). Multiply p by the orthogonal matrix R, then p′ = Rp represents the rotated point P′ (or, more precisely, the vector ${\overrightarrow {OP'}}$ is represented by column vector p′ with respect to the same Cartesian frame). If we map all points P of the body by the same matrix R in this manner, we have rotated the body. Thus, an orthogonal matrix leads to a unique rotation. Note that the Cartesian frame is fixed here and that points of the body are rotated, this is known as an active rotation. Instead, the rigid body could have been left invariant and the Cartesian frame could have been rotated, this also leads to new column vectors of the form p′ ≡ Rp, such rotations are called passive.

Properties of an orthogonal matrix

Writing out matrix products it follows that both the rows and the columns of the matrix are orthonormal (normalized and orthogonal). Indeed,

${\begin{aligned}\mathbf {R} ^{\mathrm {T} }\mathbf {R} &=\mathbf {E} \quad \Longrightarrow \quad \sum _{k=1}^{3}R_{ki}\,R_{kj}=\delta _{ij}\quad {\hbox{(columns)}}\\\mathbf {R} \mathbf {R} ^{\mathrm {T} }&=\mathbf {E} \quad \Longrightarrow \quad \sum _{k=1}^{3}R_{ik}\,R_{jk}=\delta _{ij}\quad {\hbox{(rows)}}\\\end{aligned}}$

where δ_ij is the Kronecker delta.

Orthogonal matrices come in two flavors: proper (det = 1) and improper (det = −1) rotations. Indeed, invoking some properties of determinants, one can prove

$1=\det(\mathbf {E} )=\det(\mathbf {R} ^{\mathrm {T} }\mathbf {R} )=\det(\mathbf {R} ^{\mathrm {T} })\det(\mathbf {R} )=\det(\mathbf {R} )^{2}\quad \Longrightarrow \quad \det(\mathbf {R} )=\pm 1.$

Compact notation

A compact way of presenting the same results is the following. Designate the columns of R by r₁, r₂, r₃, i.e.,

$\mathbf {R} =\left(\mathbf {r} _{1},\,\mathbf {r} _{2},\,\mathbf {r} _{3}\right)$.

The matrix R is orthogonal if

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_i^\mathrm{T} \mathbf{r}_j \equiv \mathbf{r}_i \cdot \mathbf{r}_j = \delta_{ij}, \quad i,j = 1,2,3 . }

The matrix R is a proper rotation matrix, if it is orthogonal and if r₁, r₂, r₃ form a right-handed set, i.e.,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_i \times \mathbf{r}_j = \sum_{k=1}^3 \, \varepsilon_{ijk} \mathbf{r}_k . }

Here the symbol × indicates a cross product and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon_{ijk}} is the antisymmetric Levi-Civita symbol,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \varepsilon_{123} =&\; \varepsilon_{312} = \varepsilon_{231} = 1 \\ \varepsilon_{213} =&\; \varepsilon_{321} = \varepsilon_{132} = -1 \end{align} }

and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon_{ijk} = 0} if two or more indices are equal.

The matrix R is an improper rotation matrix if its column vectors form a left-handed set, i.e.,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_i \times \mathbf{r}_j = - \sum_{k=1}^3 \, \varepsilon_{ijk} \mathbf{r}_k \; . }

The last two equations can be condensed into one equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_i \times \mathbf{r}_j = \det(\mathbf{R}) \sum_{k=1}^3 \; \varepsilon_{ijk} \mathbf{r}_k }

by virtue of the the fact that the determinant of a proper rotation matrix is 1 and of an improper rotation −1. This was proved above, an alternative proof is the following: The determinant of a 3×3 matrix with column vectors a, b, and c can be written as scalar triple product

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det\left(\mathbf{a},\,\mathbf{b},\, \mathbf{c}\right) = \mathbf{a} \cdot (\mathbf{b}\times\mathbf{c}) } .

It was just shown that for a proper rotation the columns of R are orthonormal and satisfy,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_1 \cdot (\mathbf{r}_2 \times \mathbf{r}_3 ) = \mathbf{r}_1 \cdot\left(\sum_{k=1}^3 \, \varepsilon_{23k} \, \mathbf{r}_k \right) = \varepsilon_{231} = 1 . }

Likewise the determinant is −1 for an improper rotation.

Explicit expression of rotation operator

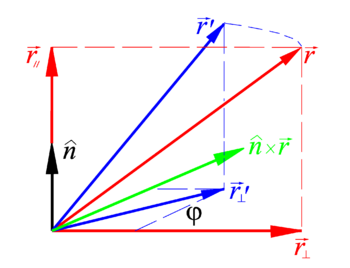
Rotation of vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \vec{r}} around axis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \hat{n}} over an angle φ. The red vectors are in the plane of drawing spanned by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \vec{r}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \hat{n}} . The blue vectors are rotated, the green cross product points away from the reader and is perpendicular to the plane of drawing.

Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP} \equiv \vec{r}} be a vector pointing from the fixed point O of a rotating rigid body to an arbitrary point P of the body. A rotation of this arbitrary vector around the unit vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} over an angle φ can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{R}(\varphi, \hat{n})(\vec{r}\,)\equiv \vec{r}\,' = \vec{r}\;\cos\phi + \hat{n} (\hat{n}\cdot\vec{r}\,)\; (1- \cos\varphi) + (\hat{n} \times \vec{r}\,) \sin\varphi . }

where • indicates an inner product and the symbol × a cross product.

It is easy to derive this result. Indeed, decompose the vector to be rotated into two components, one along the rotation axis and one perpendicular to it (see the figure on the right)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r} = \vec{r}_\parallel + \vec{r}_\perp\quad\hbox{with}\quad \vec{r}_\parallel = \hat{n} (\hat{n}\cdot\vec{r}\,), \quad \vec{r}_\perp = \vec{r}- \hat{n} (\hat{n}\cdot\vec{r}\,). }

Upon rotation the component along the axis is invariant, only the component orthogonal to the axis changes. By virtue of the fact that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{r}_\perp| = |\hat{n} \times \vec{r}\,| = \sqrt{|\vec{r}\,|^2 - (\hat{n}\cdot\vec{r}\,)^2}, }

the rotation property simply is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}_\perp \mapsto \vec{r}\,'_\perp = \cos\phi\;\vec{r}_\perp + \sin\phi\;(\hat{n}\times\vec{r}\,). }

Hence

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}\,' = \left[\vec{r}- (\hat{n}\cdot\vec{r}\,) \hat{n}\right]\cos\phi+(\hat{n}\times\vec{r}\,)\sin\phi + \hat{n} (\hat{n}\cdot\vec{r}\,). }

Some reshuffling gives the required result.

Explicit expression of rotation matrix

It will be shown that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\phi, \hat{n}) = \mathbf{E} + \sin\phi \mathbf{N} +(1-\cos\phi)\mathbf{N}^2, }

where (see cross product for more details)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{N} \equiv \begin{pmatrix} 0 & -n_z & n_y \\ n_z& 0 & -n_x \\ -n_y& n_x & 0 \end{pmatrix}\quad\hbox{and}\quad \hat{n} \equiv (\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\,) \begin{pmatrix} n_x \\ n_y \\ n_z \\ \end{pmatrix} \equiv (\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\,) \; \hat{\mathbf{n}} }

Note further that the dyadic product satisfies (as can be shown by squaring N),

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\mathbf{n}}\otimes\hat{\mathbf{n}} = \mathbf{N}^2 + \mathbf{E}, \quad\hbox{with}\quad |\hat{\mathbf{n}}| = 1 }

and that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n} (\hat{n}\cdot\vec{r}\,) \leftrightarrow (\hat{\mathbf{n}}\otimes\hat{\mathbf{n}})\;\mathbf{r} = \left(\mathbf{N}^2 + \mathbf{E}\right) \mathbf{r}. }

Translating the result of the previous section to coordinate vectors and substituting these results gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{r}' &= \left[\cos\phi\; \mathbf{E} +(1-\cos\phi)(\mathbf{N}^2 + \mathbf{E}) + \sin\phi \mathbf{N} \right] \mathbf{r} \\ &= \left[\mathbf{E} + (1-\cos\phi) \mathbf{N}^2 + \sin\phi \mathbf{N}\right] \mathbf{r}, \end{align} }

which gives the desired result for the rotation matrix. This is equation is identical to Eq. (2.6) of Biedenharn and Louck, who give credit to Leonhard Euler (ca. 1760) for this result.

The equation is a special case of the transformation properties given on p. 7 of the classical work (first edition 1904) of Whittaker. To see the correspondence with Whittaker's formula, which includes also a translation over a displacement d and who rotates the vector (x−a, y−b, z−c), we must put equal to zero: a, b, c, and d in Whittaker's equation. Furthermore he uses that the components of the unit vector n are the direction cosines of the rotation axis:

$n_{x}\equiv \cos \alpha ,\quad n_{y}\equiv \cos \beta ,\quad n_{z}\equiv \cos \gamma .$

Under these conditions the rotation becomes

${\begin{aligned}x'&=x-(1-\cos \phi )\left[x\;\sin ^{2}\alpha -y\;\cos \alpha \cos \beta -z\;\cos \alpha \cos \gamma \right]+\left[z\;\cos \beta -y\;\cos \gamma \right]\sin \phi \\y'&=y-(1-\cos \phi )\left[y\;\sin ^{2}\beta -z\;\cos \beta \cos \gamma -x\;\cos \beta \cos \alpha \right]+\left[x\;\cos \gamma -z\;\cos \alpha \right]\sin \phi \\z'&=z-(1-\cos \phi )\left[z\;\sin ^{2}\gamma -x\;\cos \gamma \cos \alpha -y\;\cos \gamma \cos \beta \right]+\left[y\;\cos \alpha -x\;\cos \beta \right]\sin \phi \\\end{aligned}}$

Vector rotation

Sometimes it is necessary to line-up a given vector in a rigid body (for instance a chemical bond in a molecule) with an external vector (for instance a coordinate vector). Let the vector in the body be f (the "from" vector) and the vector to which f must be rotated be t (the "to" vector). Let both vectors be unit vectors (length 1). From the definition of the inner product and the cross product follows that

$\mathbf {f} \cdot \mathbf {t} =\cos \phi ,\quad |\mathbf {f} \times \mathbf {t} |=\sin \phi ,$

where φ is the angle (< 180°) between the two vectors. Since the cross product f × t is a vector perpendicular to the plane of both vectors, it is easily seen that a rotation around the cross product vector over an angle φ moves f to t.

Write

$\mathbf {u} =\mathbf {f} \times \mathbf {t} \quad \Longrightarrow \quad {\hat {\mathbf {n} }}={\frac {\mathbf {u} }{\sin \phi }}.$

Define accordingly

$\mathbf {U} \;{\stackrel {\mathrm {def} }{=}}\;\sin \phi \mathbf {N} ={\begin{pmatrix}0&-u_{z}&u_{y}\\u_{z}&0&-u_{x}\\-u_{y}&u_{x}&0\end{pmatrix}}$

so that

${\begin{aligned}\mathbf {R} (\phi ,{\hat {n}})&=\mathbf {E} +\mathbf {U} +{\frac {1-\cos \phi }{\sin ^{2}\phi }}\mathbf {U} ^{2}\\&=\mathbf {E} +\mathbf {U} +{\frac {1}{1+\cos \phi }}\mathbf {U} ^{2}\\&=\cos \phi \,\mathbf {E} +\mathbf {U} +{\frac {1}{1+\cos \phi }}\mathbf {u} \otimes \mathbf {u} \\\end{aligned}}$

The last equation, which follows from U² = u⊗u − sin²φ E, is Eq. (1) of Ref. after substitution of

${\frac {1-\cos \phi }{\sin ^{2}\phi }}={\frac {1-\cos \phi }{1-\cos ^{2}\phi }}={\frac {1}{1+\cos \phi }}.$

If the vectors are parallel, f = t, then u = 0, U = 0 and f•t = cosφ = 1, so that the equation is well-defined—it gives R(φ, n) = E, as expected. Provided f and t are not anti-parallel, the matrix $\mathbf {R} (\phi ,{\hat {n}})$ can be computed easily and quickly. It requires not much more than the computation of the inner and cross product of f and t.

Case that "from" and "to" vectors are anti-parallel

If the vectors f and t are anti-parallel, f = − t, then f•t = cosφ = − 1, and the denominator in the last equation becomes zero, so that the equation is not applicable. The rotation axis u ≡ f × t = f × (−f) = 0. Clearly, a two-fold rotation (angle 180°) around any rotation axis perpendicular to f and t will map f onto −f. This freedom in choice of the two-fold axis is consistent with the indeterminacy in the equation that occurs for cosφ = −1.

Since f and t are related by inversion (with matrix −E), one could naively assume that all position vectors of the rigid body may be inverted. However, if the rigid body is not symmetric under inversion (does not have a symmetry center), inversion turns the body into a non-equivalent one. For instance, if the body is a right-hand glove, inversion will send it into a left-hand glove and as is well-known a right-hand glove differs from a left-hand glove.

Recall that f is a unit vector. If f is on the z-axis, |f_z| = 1, then the following rotation around the y-axis turns f into −f = t:

$\mathbf {R} (\pi ,{\hat {e}}_{y})\mathbf {f} ={\begin{pmatrix}-1&0&0\\0&1&0\\0&0&-1\\\end{pmatrix}}{\begin{pmatrix}0\\0\\\pm 1\end{pmatrix}}={\begin{pmatrix}0\\0\\\mp 1\end{pmatrix}}$

If f is not on the z-axis, f_z ≠ 1, then the following orthogonal matrix sends f to −f and hence gives a 180° rotation of the rigid body

$\mathbf {R} (\pi ,{\hat {e}}_{y'})\mathbf {f} ={\frac {1}{1-f_{z}^{2}}}{\begin{pmatrix}-(f_{x}^{2}-f_{y}^{2})&-2f_{x}f_{y}&0\\-2f_{x}f_{y}&(f_{x}^{2}-f_{y}^{2})&0\\0&0&-(1-f_{z}^{2})\\\end{pmatrix}}{\begin{pmatrix}f_{x}\\f_{y}\\f_{z}\end{pmatrix}}={\begin{pmatrix}-f_{x}\\-f_{y}\\-f_{z}\end{pmatrix}}$

To show this we must use relations of the type

${\frac {1}{1-f_{z}^{2}}}{\big (}-f_{x}(f_{x}^{2}-f_{y}^{2})-2f_{x}f_{y}^{2}{\big )}={\frac {-f_{x}}{1-f_{z}^{2}}}{\big (}(f_{x}^{2}-f_{y}^{2})+2f_{y}^{2}{\big )}={\frac {-f_{x}}{1-f_{z}^{2}}}(f_{x}^{2}+f_{y}^{2})={\frac {-f_{x}}{1-f_{z}^{2}}}(1-f_{z}^{2})=-f_{x}.$

Given f = (f_x, f_y, f_z), the matrix $\mathbf {R} (\pi ,{\hat {e}}_{y'})$ is easily and quickly calculated.