Talk:Monty Hall problem

External link

Richard, CZ does not allow self-promotion. Therefore I removed the link to your paper. I hope you understand this and agree with it. After some progress has been made with the main article, we may put it (together with other references) on the Bibliography subpage. --Peter Schmitt 23:18, 15 January 2011 (UTC)

I agree that we ought to see how the article progresses, but I wouldn't see a problem with adding that particular paper to the Bibliography if the math editors think it is appropriate since it is specifically about the subject and he is not selling anything. It also helps to let someone else place the link for you. D. Matt Innis 00:28, 16 January 2011 (UTC)

Agree, at a quick glance the paper does not appear to be specific self-promotion, but it should not be on the main page.

Go ahead and add it to the Bibliography page and let's encourage a maths editor to review it for appropriateness.

I'd like to see this article expanded fairly quickly; at present it doesn't tell us exactly what the Monty Hall problem is. Putting the definition as the introduction would probably be enough of a start.

Aleta Curry 00:43, 16 January 2011 (UTC)

That's about what I thought. I was, however, uncertain if current policy classifies such a link as self-promotion. Was I saying it too unfriendly? But, in any case, the link cannot replace an unwritten article. --Peter Schmitt 00:52, 16 January 2011 (UTC)

Oh, I don't know about unfriendly, but Richard is new here so I didn't want him to think his efforts were unappreciated. Aleta Curry 01:09, 16 January 2011 (UTC)

While we may indeed need to clarify the policy with an EC motion, I've never thought that a link to a clearly noncommercial page is self-promotion. This is even more the case when pointing to one's own peer-reviewed publications and presentations, which I have done -- I might not have written them if I thought there were better references. Howard C. Berkowitz 01:05, 16 January 2011 (UTC)

I had some discussion about this with Larry years ago, with respect to using one's own articles if one were a) an authority in the field or b) the only person writing in the field! His answer, basically, was 'use common sense and ask an(other) Editor to review/confirm'.

Aleta Curry 01:09, 16 January 2011 (UTC)

Thanks everyone. The point of the reference was just to be a resource for anyone interested in joining in. Over on Wikipedia a fight has been going on for two years, basically between laypersons who find a short intuitive solution of MHP completely satsfying, and mathematicians who dogmatically insist on a tricky solution using Bayes theorem. My own modest contribution (he said modestly) was merely to present the mathematical facts of the matter and go some way to resolving the Wikipedia conflict. Partly, by creating a "reliable source" (wikipeda terminology) for both sides of that battle. Partly by showing that the "full conditional solution" can be obtained by making one small step from the "popular simple solution" by the use of symmetry - a neat trick which I learnt from our friend Boris in this context! However the paper is too mathematical for most laypersons.

I think it's challenging to get across to laypersons what the difference is between the simple solutions and the conditional solutions, as they are often referred to. More below.

Problem variant as a cartoon

I must share a memorable cartoon idea based on this problem, from Playboy (I read it for the cartoons). The problem is reduced to two doors, and the contestant is faced with legends of "damned if you do" and "damned if you don't". Monty Hall, the game show host, is in devil garb, prodding the contestant with a pitchfork. Howard C. Berkowitz 00:12, 16 January 2011 (UTC)

As an aside, is Monty Hall his real name, or was it a joke referring to 3 card Monte? Aleta Curry 01:09, 16 January 2011 (UTC)

I looked it up, Monte Hall was apparently the stage name for Monte Halperin of the TV game show, "Let's make a Deal", so it looks like his mother was the one pulling the 3 card Monte :)D. Matt Innis 01:28, 16 January 2011 (UTC)

There is question related to it: Should this be "Monty Hall Problem" or "Monty Hall problem". I tend to the latter, but this is a question for language experts. --Peter Schmitt 01:33, 16 January 2011 (UTC)

I remember that! I was...ahem...two years old, of course, but....Aleta Curry 01:34, 16 January 2011 (UTC)

It would be nice, @Howard, to find that cartoon on internet! @Peter, Regarding the P for problem: as a rusty native English speaker who was never all that good at spelling or grammar, I'd say that in plain text, whether you write Monty Hall Problem or Monty Hall problem depends on context. If you are writing about many different problems, then the Monty Hall problem is just one of those many problems. However when you are writing about The Monty Hall Problem capitalization of the P is appropriate. The word is part of the common name of one individual problem. Richard D. Gill 13:07, 26 January 2011 (UTC)

Hmmm...I think Playboy rather than New Yorker. When I read Playboy, it is for the cartoons. Howard C. Berkowitz 21:25, 26 January 2011 (UTC)

Proposal for main content

Apart from history, sources, variants, and so on, the main content of the article should obviously be the presentation of a solution to MHP. The challenge is to simultaneously satisfy mathematical pedants and be intelligible to ordinary lay-persons. This requires an almost purely verbal solution, using only plain words of everyday English, which does however, sentence by sentence, cover every single logical step, including explicit use of all necessary assumptions. That's what I plan to write first. Now. Richard D. Gill 11:22, 26 January 2011 (UTC)

First try done. Please edit or comment. Richard D. Gill 13:08, 26 January 2011 (UTC)

Better than WP, which is however not a compliment: on WP it is too bad. Well, this is just good, I think so.

A remark: you mention Bayesian probability (and I understand why), but just above that you use frequentist probability (you count the winning ratio in the long run!). Some readers may be confused. --Boris Tsirelson 21:03, 26 January 2011 (UTC)

You're right. I should remark explicitly on the "paradigm shift". It was kind of deliberate. I think that the "standard" uniformity assumptions of MHP are only well-justified within a subjectivist notion of probability. For a frequentist, it is harder to come up with any probability model or at all, and even if it does make some sense, the probabilities cannot be considered as known in advace. But the frequentist picture is also valuable. Personally, I understand the arithmetic of relative frequencies much better than the "logic" of subjective probability. Fortunately, whatever your personal choice, subjectivist and frequentist probability satisfy the same rules, so I can always give a frequentist story about a subjectivist probability inspired model.

One of the wikipedia MHP editors wrote "no one who thinks seriously about MHP cannot avoid pondering on the meaning of probability". My own opinion is that the infinitely many repetitions of the frequentist are equally imaginary to the "parallel worlds" of the subjectivist. Both are equally meta-physical, thus the choice is a matter of opinion, of religion, of choice of meta-phor. The important thing is that we use probability in scientific discourse hence we need some kind of inter-subjectivity. You have to make the repetitions, of whichever kind, appealing and understandable to the people you want to communicate with. Richard D. Gill 23:56, 26 January 2011 (UTC)

I would find a truth table of some sort particularly illustrative in the explaination in the first paragraph or two, showing the 3 possible car locations, the host's choice(s) of doors to open, and the contestants win/loss result of switch/no switch. David E. Volk 19:36, 27 January 2011 (UTC)

I don't think that a "truth table" or, rather, a tree showing the possibilities is useful. It looks impressive but makes it also look more complicated than it is. There are, essentially, only two distinct cases - the door first chosen is the winning one, or it is not ... (For those looking for such a diagram, it could, perhaps, be put on a subpage.) --Peter Schmitt 20:41, 27 January 2011 (UTC)

Peter, if we were writing for PhD mathematicians who can obviously grasp that point, I would agree, but others get the aha moment by looking at the possible outcomes. David E. Volk 21:13, 27 January 2011 (UTC)

I very much doubt that a table (as in your sandbox) makes it easier for a "non-mathematician". I rather expect that the non-initiated looks at it and thinks "well, if the mathematicians say that thse are the formulas to use, then I tend to believe it.) The table does not help to understand the crucial point.

I think it is easier to argue as informally as possible: Your chances are 1 in 3 (or 1 to 2) to choose the winning door first, thus chances are 2 in 3 (or 2 to 1) that you have not chosen the winning door and switching opens the winning door.

Everyone understands that you have a 1/3 chance at the onset, and 2/3 chance of being wrong at the onset, but almost everyone fails to understand why the opening of one door, thus leaving the car behind only one of two closed doors, does not equal a 50:50 chance. In other words, they fail to see why opening one of the doors does not change your odds. A layman thinks, 1 car in 1 of 2 locations = even odds.

In this particular problem, the general masses heard the answer of the mathematicians and said no ****** way!. They did not believe that the solution was correct, and still don't after much explaination. David E. Volk 21:54, 27 January 2011 (UTC)

I know the history of the problem and the many disputes caused by it. But calculations, the use of formulas, do not help to understand the problem. They may help you to convince the "general masses" because they tend to believe in mathematical formulas (without bothering to understand them), but not help them to better grasp the solution. --Peter Schmitt 22:19, 27 January 2011 (UTC)

It's clear from the wikipedia MHP wars that different readers need different ways to get their minds around the problem. Some have to see a table of numbers. Some have to see a formal mathematical derivation. Others need the briefest possible verbal argument, anything more overloads their minds. The MHP pages here should, I suppose, also cater for all tastes, while keeping the structure clean and mean.

MHP wars on wikipedia in a nutshell

Consider this four step informal/intutive "good" solution to MHP. Do you think the third step - placed in parentheses - is necessary or unnecessary?

• 2/3 of the time the contestant will select a goat

• The host opening a door to reveal a goat doesn't change this.

• (The door being opened being door 3 doesn't change this either)

• Therefore the contestant should switch

Step 1 uses only "car is hidden at random"

Step 3 uses the symmetry (the probability assumptions don't change on renumbering the doors) of adding to the previously used assumption also the assumption "host choice 50-50"

The four-step argument is intuitive and mathematically rigorous at the same time - each step can be converted into formal mathematical language via the use of Bayes' rule.

The "simple solution" or "unconditional solution" corresponds to removing Step 3, the "conditional solution" corresponds to keeping it. Richard D. Gill 08:23, 28 January 2011 (UTC)

We see how the simple solution does not require the full assumption set: the advantages and disadvantages of both solutions are plainly visible.

Removing step 3 is not really a problem. The problem occurs, I think, in believing that Step 2 is true. It needs to be explained in terms of the possible choices available to the host as to which doors can be opened. If the contestant chooses correctly, the host has 2 choices of which door to open, and if the contestant chooses incorrectly the host has only 1 choice of door to open. David E. Volk 15:18, 28 January 2011 (UTC)

This is subtle, @David! And depends rather crucially on how Step 2 is to be understood! I meant: a door is opened revealing a goat, but the number of that door has not yet been revealed to the contestant. With this understanding, Step 2 is easily seen to be true, since it speaks of "a door", not of a specific door. Whether or not the car is behind Door 1, the host will certainly open a door a reveal a goat. The fact that a door is opened revealing a goat does not (under the conditions of the game) give us any information regarding the question "is the car behind Door 1, yes or no?"

So once we have completed Step 1 and Step 2 we have arrived at what some people over on wikipedia call "the simple solution". Given a door has been opened revealing a goat (but the identity of the opened door is not yet known), the odds are still 2:1 that Door 1 hides a goat. Hence switching to the other door gives the car with probability 2/3.

So far, we ignored the number of the door opened (at least, that was my intention). Let's look at Step 3 - the one in parentheses, which many authors of "popular" solutions ignore. We have fixed that the player chose Door 1. We know in advance that the host is going to open either Door 2 or Door 3, but not which. By the symmetry of the problem with respect to Doors 2 and 3, (including the assumption that the two host's choices are equally likely if he has a choice), the probability the host opens Door 3 given the car is behind Door 1 is 50%, and the probability the host opens Door 3 given the car is not behind Door 1 is 50%. Thus the identity of the Door being opened contains no information about whether or not the car is behind Door 1 - Door 3 has exactly the same chance of being opened under either hypothesis.

I learnt this way of solving MHP from wikipedia: Garry Kanter presented the pithy three step solution there i.e. excluding my parenthetical Step 3 !

What I like about this approach is that it is at the same time intuitive and mathematically formalizable. Rather than doing mindless computations using the formal definition of conditional probability (which is what formal solutions using Bayes's theorem in its common text-book form do) it uses the very intuitive Bayes' rule: posterior odds equals prior odds times likelihood ratio. And it is crafted so that the likelihood ratio is always 1, that is to say, each new piece of information has the same chance under the two competing hypotheses, hence is actually non-information. From an educationalist point of view, I would like to see ordinary people be able to gain some probabilistic intuition by becoming familiar with and hence being able to internalize Bayes' rule.

There is trickiness in the ambiguous wording "a door is opened". Line 2 has to have added to it "the number of the opened door is not yet revealed to the contestant".

People with a formal training in probability tend to find Step 3 absolutely crucial. They insist that the competitor's choice must be guided by the conditional probability that the car is behind Door 2 given the host has opened Door 3. Those without formal training in probability theory tend to see absolutely no value in it, because of the combination of semantic ambiguity and the mathematical fact that the number of the door opened is indeed irrelevant regarding the decision of whether to switch of stay. (Which can be seen in many ways, and used in a formal proof in many ways - at the outset or at the end or somewhere in the middle).

In mathematical language: given the contestant has chosen Door 1, whether or not the car is behind Door 1 is statistically independent of whether the host opens Door 2 or Door 3.Richard D. Gill 20:39, 28 January 2011 (UTC)

Let us put a hypothetical Step 1a between Steps 1 and 2: The host asks you if you want to switch provided you win if the car is behind one of the two doors. Switching clearly doubles the chances. After you switched, the host teases you by opening the (a) losing door first before revealing whether you have won. Since it is already decided whether you have won this does not change the odds. --Peter Schmitt 21:33, 28 January 2011 (UTC)

Another problem

I recall when the original vos Savant column came out and the thousands of letters it generated. To me, the biggest problem was believing that the woman with supposedly the highest IQ in the world was actually named "von Savant" (I mistakenly thought it was "von", not "vos".) It seemed to me like a supreme put-on. It wasn't until many years later, when the Internet, and, I suppose, Wikipedia, had come along, that I Googled this improbable name and discovered, to my astonishment, that it was an actual name. As if the *stupidest* person in the world was actually named George vos Dumb.... Hayford Peirce 21:01, 27 January 2011 (UTC)

New Guy Here...

Hi, I've been very active in the Wikipedia MHP discussions for 2+ years. No real CV to speak of, just a lot of OCD.

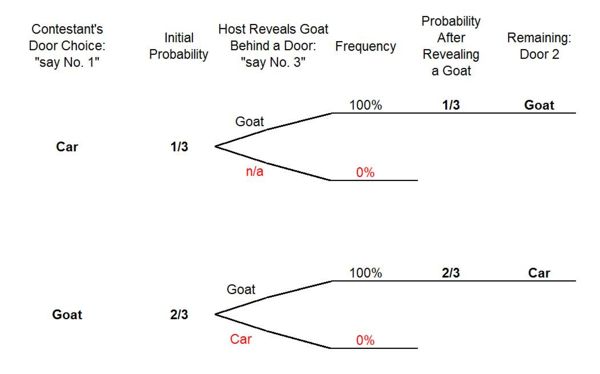
I prepared this decision tree to explain the 'simple solutions'. The other Wikipedia editors did not feel it was worthy of inclusion in the article. It is derived from Carlton's simple solution, and from Morgan's (false) F5.

Simple solution decision tree

I think it is an informative representation of what has been referred to as the (elusive) 'Peaceful Co-existance' of the simple and the conditional solutions. I welcome any comments as to it's suitability for and benefit to the article. Garry L. Kanter 15:30, 28 January 2011 (UTC)

I think the words "say Door 2" and "Door 3" should be deleted from the picture, because the host's choice is not part of the probability story told in the picture. You could give the picture without those words, and then remark that by symmetry the number of the door opened by the host doesn't change the likelihood that the car is behind the door chosen by the player. But then I don't really see the added value in having the picture.

The thoughts of some other citizens, both experts and laymen with regards to probability, would be interesting. Richard D. Gill 15:41, 30 January 2011 (UTC)

Should The Contestant Switch? - A Simple Solution To The Door 3 Has Been Opened Problem - Without The 50/50 Host Bias Premise

Preamble

What you are about to read comes from the mind of a lay person. It is unvetted. But I think it is valid, correct, and complete.

I will leave out some supporting arguments for clarity, but welcome questions, and I think I am prepared for them.

This solution relies on Logic/Philosophy rather than Conditional Probability.

As I am often told that I misuse them, I will do my best to avoid technical terms and jargon.

The Paradox

• "Why is it 2/3 & 1/3 rather than 1/2 & 1/2?"

The Problem Statement Of Interest

• "Suppose you are on a game show..."

The Critical Premise

The only valid host biases (when faced with 2 goats) that can be incorporated into the Monty Hall Problem paradox are

• 50/50 - as per Selvin's 2nd letter
• unstated - as per vos Savant, as interpreted by Morgan
• Any hypothetical host bias, a la Morgan, is for academic purposes only, or to show the greater generalization capabilities of formal conditional solutions

The Differences Between Logic and Probability

The Result

• The contestant faces a situation where a *decision* is required, not a *precise numeric calculation*
• Being on a game show, the contestant has the presumption that the car distribution and the host bias are random
• If the above statement were not the case, the contestant *will not* be informed of any other method of car distribution or how the host decides between 2 goats

Different Standards

• From what I can gather from 2+ years of discussions, relying upon 'Symmetry' or 'random and uniform' in probability requires a *certainty* that events are equally likely
• From what I have experienced in real life, and from solving puzzles, a Logical model only requires the *the absence of evidence that indicates otherwise*

(RDG-1) I think you have misunderstood something. You are on the game show and know nothing except for the rules, which are: the three doors hide two goats and one car. You will choose a door. The host will open another door and reveal a goat and offer a switch - which he can always do since he knows the location of the car. For you therefore the host is equally likely to open Door 2 or Door 3. This is sometimes called "logical probability". There ought to be an article on it on wikipedia or citizendium or both. I suppose by being certain that the two doors are equally likely you would mean that a totally reliable informant has told you that the host chooses which door to open, if he has a choice, by using a fair randomizer. That would certainly imply that for you the host is equally likely to open either door. But it is a rather special case, and it doesn't apply to MHP since we are not given any such information. Richard D. Gill 13:17, 30 January 2011 (UTC)

Richard, maybe you could directly address the 2 statements I made? I'm simply tying to differentiate between being given premises like these from K & W:

• 'The car and the goats were placed randomly behind the doors before the show.'
• 'If both remaining doors have goats behind them, he chooses one [uniformly] at random.'

and these, that I devised about a game show, which I think you labeled as 'logical probability':

• 'The contestant, having no information as to where the car is, [and in the absence of evidence to the contrary] assumes each door is equally likely.'
• 'The contestant being unaware of the host's strategy when he has 2 goats, [and in the absence of evidence to the contrary] assumes each door is equally likely to be opened.'

I'm trying to understand if 'logical probability' can be used for the symmetry portion of the simple solution + symmetry + tlop solutions. Or, what is the difference between 'logical probability' and the 'special case of the fair randomizer' (or K & W's premises)? Or, if using the the logic that all 6 door pairings are equally likely, then an indifferent simple solution solves the specific door 1 and door 3 conditional problem by itself. Garry L. Kanter 13:37, 30 January 2011 (UTC)

The Critical Reasoning

• The contestant has no reason to think any of the 6 'door selected and door opened pairings' have different likelihoods than the other 5, each at 2/3 & 1/3
• Door 1 selected and door 3 opened is one of the 6 pairings described above
• [extra reasoning] The contestant has no reason to think the door 1 and door 3 pairing is somehow contrary to the 2/3 & 1/3 he calculated, and that his door has a (much) greater than 50% likelihood of being the car

(RDG-2) I earlier found it difficult to understand what you meant about the 6 different pairings having different likelihoods. You were talking about the likelihood of the car being behind the chosen door or not. You're saying that there is no reason to think that for any of the six different values of (door chosen, door opened, door remaining) the likelihood that it corresponds to (car, goat, goat) or to (goat, goat, car) is different. This is the "symmetry argument" again, applied to your logical probabilities. Here you use it to show that the numbers on the doors are independent of the relationship between their manifest and their hidden roles, by the symmetry of your knowledge or lack thereof. The initially chosen door has a chance of 2/3 to hide a goat. The numbers written on this door and on the door opened by the host don't change this chance. The contestant's chance of his first door hiding a goat remain 2/3, whatever the pairing. Richard D. Gill 13:26, 30 January 2011 (UTC)

I'm trying to point out that the contestant *wouldn't* have any reason to think any of the 6 pairings (contestant's door, remaining door) have odds other than 1/3 & 2/3. I'm trying to present a rigorous logical argument to explain why the contestant would switch for the specific door 1 and door 3 pairing, rather than using a simple solution + symmetry + tlop. Garry L. Kanter 13:44, 30 January 2011 (UTC)

The Simple Solution

• The contestant knows that he would select a goat 2/3 of the time
• The contestant receives no information as to the location of the car when the host opens door 3 to reveal a goat

The original distribution of the goats is 2/3, 2/3, 2/3

The contestant selecting a door does not change the above

• The contestant has no reason to think the door 1 and door 3 pairing has a likelihood other than 2/3 & 1/3
• The contestant doubles his likelihood of winning the car by switching

The Conclusion - Another Paradox

• I've shown that absent the 50/50 host bias premise, the simple solutions return the result 2/3 & 1/3 for the problem where the host revealed a goat behind door 3
• The formal conditional solutions cannot calculate any probabilities without a host bias premise to plug in
• Morgan is wrong that the simple solutions, without the 50/50 host bias premise do not solve the door 1 selected & door 3 revealed MHP.
• In fact, simple solutions are the only solutions that are consistent with the paradox 'Why is it 2/3 & 1/3 rather than 1/2 & 1/2 ?" without requiring a 50/50 host bias premise.

Actually, I may not have left out any supporting stuff. I welcome your responses, below. Garry L. Kanter 01:39, 29 January 2011 (UTC)

Response by Richard Gill

See responses (RDG-1) and (RDG-2) above. It seems to me that your arguments are in essence the same as the simple solution ("switching gives the car with probability 2/3") completed with the symmetry argument ("switching gives the car with conditional probability 2/3, conditional on the door number of the initial player choice and of the door opened by the host").

Splendid! What I have always wanted to see is a translation of the conditional solution into ordinary layperson's language, and that is what you have been pushing for too. Richard D. Gill 13:37, 30 January 2011 (UTC)

No, I'm trying to make the case that using logic rather than probability, that the [conditional] simple solutions, on their own, solve the conditional door 3 has been opened problem. That is, they don't need to rely on symmetry to do whatever it is you and Boris say simple + symmetry + lotp accomplish. Garry L. Kanter 13:50, 30 January 2011 (UTC)

You are using logic first to argue that a certain event has a likelihood of 2/3 (2/3 chance that your initial choice hides a goat) and then to show that this likelihood can't depend on some further information (the identity of the door opened by the host). I would say "no reason the odds should be different for any of the six pairings" is the same as saying that by symmetry, the conditional probability must be the same as the unconditional.

Students of probability might find the hint (law of total probability) useful to show that the calculus of probability does conform to one's logical expectations. The old hands don't need the hint.

Well, it will be interesting to see what some further citizens think, both those who are expert in probability, and those who are not. Richard D. Gill 15:25, 30 January 2011 (UTC)

I have no background in maths, statistics etc. and took a while to understand the problem (days, actually). What made it click for me was the part which mentions playing the game many times. I imagined 99 repetitions of the game with the car randomly behind any of the doors each time. Obviously, if the player sticks to door #1 each time, he'll win about 33 times, on average. But if he switches on all 99 plays, he'll lose the car only on the roughly 33 occasions that it really was behind door #1 to start with, i.e. he wins about 66 out of 99 times, which is 2/3 odds. John Stephenson 15:57, 30 January 2011 (UTC)

The table at the end of the article

The first column appears to add to 1 1/3. In the next to last column, I think row 1 should have a value of 0 or n/a. In the last column, I think row 4 should have a value of 0 or n/a.Garry L. Kanter 12:45, 30 January 2011 (UTC)

The first two cells of the first column are the same. They should be merged into one box. And I think it would be better to write "Probability..." rather than "p=.." everywhere. The "p" in each column is the probability or conditional probability or joint probability of something different in each column. This table is really the same as the original Carlton decision tree. Richard D. Gill 15:31, 30 January 2011 (UTC)