Periodic function: Difference between revisions
Jump to navigation
Jump to search
imported>Aleksander Stos m (categories) |
imported>Jitse Niesen (fix sawtooth wave definition) |
||
| Line 1: | Line 1: | ||
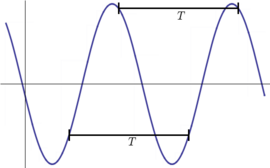
[[Image:periodicFunction.png|thumb|270px|Example of a periodic function, with period <math>T</math>. If you choose any point on the function and then move to the left or right by <math>T</math>, you will find the same value as at the original point.]] | [[Image:periodicFunction.png|thumb|270px|Example of a periodic function, with period <math>T</math>. If you choose any point on the function and then move to the left or right by <math>T</math>, you will find the same value as at the original point.]] | ||
In [[mathematics]] a | In [[mathematics]] a '''periodic function''' is a [[function]] that repeats itself after a while, and indefinitely. | ||
The mathematical definition of this is that <math>f(t)</math> is periodic with [[period]] <math>T</math> | The mathematical definition of this is that <math>f(t)</math> is periodic with [[period]] <math>T</math> | ||
if | if | ||
| Line 11: | Line 11: | ||
A sawtooth wave is a periodic function that can be described by | A sawtooth wave is a periodic function that can be described by | ||
: <math> f(x) = \begin{cases} |x-1| & \text{if } -1<x<1, \\ f(x+2) & \text{if } x \le -1, \\ f(x-2) & \text{if } x \ge 1. \end{cases} </math> | |||
[[Category: Mathematics Workgroup]] | [[Category: Mathematics Workgroup]] | ||
[[Category: CZ Live]] | [[Category: CZ Live]] | ||
Revision as of 00:54, 11 September 2007
In mathematics a periodic function is a function that repeats itself after a while, and indefinitely. The mathematical definition of this is that is periodic with period if
Common examples of periodic functions are and , which both have period .
A sawtooth wave is a periodic function that can be described by