Law of sines: Difference between revisions
Jump to navigation
Jump to search

imported>David E. Volk m (subpages stuff) |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
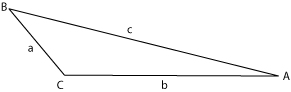
In [[geometry]] the '''law of sines''' is useful for calculating one side or angle of any triangle, when five of the six angles and sides are known. It can be stated as | |||
:''See [[Sine rule]] for a proof''. | |||
In [[geometry]] the '''law of sines''' (also known as sine rule) is useful for calculating one side or angle of any triangle, when five of the six angles and sides are known. It can be stated as | |||
:<math> \frac{\sin {A}}{a} = \frac{\sin {B}}{b} = \frac{\sin{C}}{c} </math> | :<math> \frac{\sin {A}}{a} = \frac{\sin {B}}{b} = \frac{\sin{C}}{c} </math> | ||
Revision as of 09:20, 18 October 2008
- See Sine rule for a proof.
In geometry the law of sines (also known as sine rule) is useful for calculating one side or angle of any triangle, when five of the six angles and sides are known. It can be stated as
where the lengths , , and correspond to the sides opposite the respective angles , , and as shown in the image.