Area of a triangle: Difference between revisions
Jump to navigation
Jump to search
imported>Olier Raby (Cat.) |
imported>Matt Mahlmann m (wfy and typos) |
||
| Line 1: | Line 1: | ||
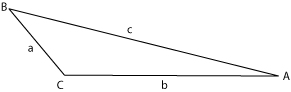
The area of any triangle can be calculated using the following equation: | The area of any [[triangle]] can be calculated using the following equation: | ||
<math> Area = \left(\frac{1}{2}\right)bc (sin A) = \left(\frac{1}{2}\right)ac (sin B) = \left(\frac{1}{2}\right)ab (sin C) </math> | <math> Area = \left(\frac{1}{2}\right)bc (sin A) = \left(\frac{1}{2}\right)ac (sin B) = \left(\frac{1}{2}\right)ab (sin C) </math> | ||
| Line 9: | Line 9: | ||
== Right triangles == | == Right triangles == | ||
For right triangles, the angle C, opposite the | For [[right triangle|right triangles]], the angle C, opposite the [[hypotenuse]] (c), is 90 degrees. The sine of 90 degrees is 1, so the equation reduces to: | ||
Revision as of 17:26, 2 November 2007
The area of any triangle can be calculated using the following equation:
Right triangles
For right triangles, the angle C, opposite the hypotenuse (c), is 90 degrees. The sine of 90 degrees is 1, so the equation reduces to: