Displacement current: Difference between revisions
imported>Paul Wormer (New page: {{subpages}} In physics, more particular in the theory of electromagnetism, the '''displacement current''' is the time derivative of the electric displacement '''D'''. It was i...) |
imported>Paul Wormer |
||
| Line 3: | Line 3: | ||
==Explanation== | ==Explanation== | ||
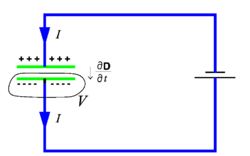
[[Image:Displacement current.png|right|thumb|250px|Charging of a parallel-plate capacitor (green plates) with current ''i''. ''V'' indicates a volume enveloped by a closed surface.]] | [[Image:Displacement current.png|right|thumb|250px|Charging of a parallel-plate capacitor (green plates) with current ''i''. ''V'' indicates a volume enveloped by a closed surface.]] | ||
In the figure on the right a [[capacitor]] (with green plates) is charged by an [[electric current]] ''i''. The conduction current ''i'' is related to the current density '''j'''('''r''') by a surface integral. Since '''j''' is everywhere zero, except over the surface of the wire (blue in the figure), one may integrate over the whole closed surface of the volume ''V'' to get ''i'', | |||
:<math> | :<math> | ||
i = \ | i = \iint_{\mathrm{closed}\atop\mathrm{surface}} \mathbf{j}(\mathbf{r})\cdot d\mathbf{S} = \iiint_V \boldsymbol{\nabla} \cdot \mathbf{j}(\mathbf{r})\, dv, | ||
</math> | </math> | ||
where the last equality follows by application of the [[divergence theorem]] of Gauss. | where the last equality follows by application of the [[divergence theorem]] of Gauss. | ||
The surface integral contains the [[inner product]] between the current density '''j''' (a vector) and a vector orthogonal to the infinitesimal surface element ''dS''. The orthogonal vector has length ''dS''. The conduction current ''i'' | The surface integral contains the [[inner product]] between the current density '''j''' (a vector) and a vector d'''S''' orthogonal to the infinitesimal surface element ''dS''. The orthogonal vector has length ''dS''. The conduction current ''i'' gives the rate of change of electric charge in the volume ''V''. Clearly, ''i'' is non-zero during the time that the capacitor is charging. | ||
[[Ampère's law]] in differential form states that | [[Ampère's law]] in differential form states that | ||
:<math> | :<math> | ||
\boldsymbol{\nabla} \times \mathbf{H} = \mathbf{j}, | \boldsymbol{\nabla} \times \mathbf{H}(\mathbf{r}) = \mathbf{j}(\mathbf{r}), | ||
</math> | </math> | ||
where '''H''' is the [[magnetic field]]. Since the divergence of the curl is zero, | where '''H'''('''r''') is the [[magnetic field]]. Since the divergence of the curl is always zero, | ||
:<math> | :<math> | ||
\boldsymbol{\nabla}\cdot(\boldsymbol{\nabla} \times \mathbf{H}) = \boldsymbol{\nabla}\cdot \mathbf{j} = 0, | \boldsymbol{\nabla}\cdot(\boldsymbol{\nabla} \times \mathbf{H}) = \boldsymbol{\nabla}\cdot \mathbf{j} = 0, | ||
| Line 20: | Line 21: | ||
it follows that | it follows that | ||
:<math> | :<math> | ||
i = \iiint_V \boldsymbol{\nabla} \cdot \mathbf{j}\, dv = 0 | i = \iiint_V \boldsymbol{\nabla} \cdot \mathbf{j}(\mathbf{r})\, dv = 0 | ||
</math> | </math> | ||
at all times, in contradiction to what was just stated. It follows that Ampère's law is in error, or is at least incomplete. | at all times, in contradiction to what was just stated. It follows that Ampère's law is in error, or is at least incomplete. | ||
| Line 38: | Line 39: | ||
\boldsymbol{\nabla}\cdot\left( \mathbf{j} + \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t} \right) = 0. | \boldsymbol{\nabla}\cdot\left( \mathbf{j} + \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t} \right) = 0. | ||
</math> | </math> | ||
Maxwell | So, Maxwell realized that the conduction current leaving the volume ''V'' was compensated by the displacement current entering ''V'', which is why he added the displacement current to the conduction current density, modifying Ampère's law to | ||
:<math> | :<math> | ||
\boldsymbol{\nabla} \times \mathbf{H} = \mathbf{j} + \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t}, \qquad\qquad\qquad\qquad(1) | \boldsymbol{\nabla} \times \mathbf{H} = \mathbf{j} + \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t}, \qquad\qquad\qquad\qquad\qquad\qquad(1) | ||
</math> | </math> | ||
with | with | ||
Revision as of 03:37, 4 July 2008
In physics, more particular in the theory of electromagnetism, the displacement current is the time derivative of the electric displacement D. It was introduced by James Clerk Maxwell as a correction to Ampère's law. It is the displacement current that gives rise to electromagnetic waves.
Explanation
In the figure on the right a capacitor (with green plates) is charged by an electric current i. The conduction current i is related to the current density j(r) by a surface integral. Since j is everywhere zero, except over the surface of the wire (blue in the figure), one may integrate over the whole closed surface of the volume V to get i,
where the last equality follows by application of the divergence theorem of Gauss. The surface integral contains the inner product between the current density j (a vector) and a vector dS orthogonal to the infinitesimal surface element dS. The orthogonal vector has length dS. The conduction current i gives the rate of change of electric charge in the volume V. Clearly, i is non-zero during the time that the capacitor is charging.
Ampère's law in differential form states that
where H(r) is the magnetic field. Since the divergence of the curl is always zero,
it follows that
at all times, in contradiction to what was just stated. It follows that Ampère's law is in error, or is at least incomplete.
Maxwell was the first to notice this and he also saw how to fix it by application of the continuity equation. This equation states that the rate of change of charge density is proportional to the the divergence of the current density
The electrostatic law of Gauss states
so that
So, Maxwell realized that the conduction current leaving the volume V was compensated by the displacement current entering V, which is why he added the displacement current to the conduction current density, modifying Ampère's law to
with
Equation (1) is one of Maxwell's equations formulated by him in 1864 and still accepted as universally valid.