Displacement current: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer (current density j --> J) |
||
| Line 4: | Line 4: | ||
==Explanation== | ==Explanation== | ||
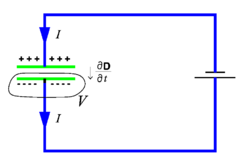
[[Image:Displacement current.png|right|thumb|250px|Charging of a parallel-plate capacitor (green plates) with current ''i''. ''V'' indicates a volume enveloped by a closed surface.]] | [[Image:Displacement current.png|right|thumb|250px|Charging of a parallel-plate capacitor (green plates) with current ''i''. ''V'' indicates a volume enveloped by a closed surface.]] | ||
In the figure on the right a [[capacitor]] (with green plates) is charged by an [[electric current]] ''i''. The conduction current ''i'' is related to the current density ''' | In the figure on the right a [[capacitor]] (with green plates) is charged by an [[electric current]] ''i''. The conduction current ''i'' is related to the current density '''J'''('''r''') by a surface integral. Since '''J''' is everywhere zero, except over the surface of the wire (blue in the figure), one may integrate over the whole closed surface of the volume ''V'' to get ''i'', | ||
:<math> | :<math> | ||
i = \iint_{\mathrm{closed}\atop\mathrm{surface}} \mathbf{ | i = \iint_{\mathrm{closed}\atop\mathrm{surface}} \mathbf{J}(\mathbf{r})\cdot d\mathbf{S} = \iiint_V \boldsymbol{\nabla} \cdot \mathbf{J}(\mathbf{r})\, dv, | ||
</math> | </math> | ||
where the last equality follows by application of the [[divergence theorem]] of Gauss. | where the last equality follows by application of the [[divergence theorem]] of Gauss. | ||
The surface integral contains the [[inner product]] between the current density ''' | The surface integral contains the [[inner product]] between the current density '''J''' (a vector) and a vector d'''S''' orthogonal to the infinitesimal surface element ''dS''. The orthogonal vector has length ''dS''. The conduction current ''i'' gives the rate of change of electric charge in the volume ''V''. Clearly, ''i'' is non-zero during the time that the capacitor is charging. | ||
[[Ampère's law]] in differential form states that | [[Ampère's law]] in differential form states that | ||
:<math> | :<math> | ||
\boldsymbol{\nabla} \times \mathbf{H}(\mathbf{r}) = \mathbf{ | \boldsymbol{\nabla} \times \mathbf{H}(\mathbf{r}) = \mathbf{J}(\mathbf{r}), | ||
</math> | </math> | ||
where '''H'''('''r''') is the [[magnetic field]]. Since the divergence of the curl is always zero, | where '''H'''('''r''') is the [[magnetic field]]. Since the divergence of the curl is always zero, | ||
:<math> | :<math> | ||
\boldsymbol{\nabla}\cdot(\boldsymbol{\nabla} \times \mathbf{H}) = \boldsymbol{\nabla}\cdot \mathbf{ | \boldsymbol{\nabla}\cdot(\boldsymbol{\nabla} \times \mathbf{H}) = \boldsymbol{\nabla}\cdot \mathbf{J}(\mathbf{r}) = 0, | ||
</math> | </math> | ||
it follows that | it follows that | ||
:<math> | :<math> | ||
i = \iiint_V \boldsymbol{\nabla} \cdot \mathbf{ | i = \iiint_V \boldsymbol{\nabla} \cdot \mathbf{J}(\mathbf{r})\, dv = 0 | ||
</math> | </math> | ||
at all times, in contradiction to what was just stated. Thus, Ampère's law is in error, or at least is incomplete. | at all times, in contradiction to what was just stated. Thus, Ampère's law is in error, or at least is incomplete. | ||
| Line 27: | Line 27: | ||
Maxwell was the first to notice this and he also saw how to fix it by application of the [[continuity equation]]. This equation states that the rate of change of a charge density is proportional to the the divergence of the current density, | Maxwell was the first to notice this and he also saw how to fix it by application of the [[continuity equation]]. This equation states that the rate of change of a charge density is proportional to the the divergence of the current density, | ||
:<math> | :<math> | ||
\boldsymbol{\nabla}\cdot \mathbf{ | \boldsymbol{\nabla}\cdot \mathbf{J} + \frac{\partial \rho}{\partial t} = 0. | ||
</math> | </math> | ||
The electrostatic [[Gauss' law (electrostatics)|law of Gauss]] states | The electrostatic [[Gauss' law (electrostatics)|law of Gauss]] states | ||
| Line 37: | Line 37: | ||
\frac{\partial \rho}{\partial t} = \boldsymbol{\nabla}\cdot \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t}, | \frac{\partial \rho}{\partial t} = \boldsymbol{\nabla}\cdot \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t}, | ||
\qquad\hbox{and}\qquad | \qquad\hbox{and}\qquad | ||
\boldsymbol{\nabla}\cdot\left( \mathbf{ | \boldsymbol{\nabla}\cdot\left( \mathbf{J} + \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t} \right) = 0. | ||
</math> | </math> | ||
So, Maxwell realized that the conduction current leaving the volume ''V'' was compensated by the displacement current entering ''V'', which is why he added the displacement current to the conduction current density, modifying Ampère's law to | So, Maxwell realized that the conduction current leaving the volume ''V'' was compensated by the displacement current entering ''V'', which is why he added the displacement current to the conduction current density, modifying Ampère's law to | ||
:<math> | :<math> | ||
\boldsymbol{\nabla} \times \mathbf{H}(\mathbf{r}) = \mathbf{ | \boldsymbol{\nabla} \times \mathbf{H}(\mathbf{r}) = \mathbf{J}(\mathbf{r}) + \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t}, \qquad\qquad\qquad\qquad\qquad\qquad(1) | ||
</math> | </math> | ||
with | with | ||
:<math> | :<math> | ||
\boldsymbol{\nabla}\cdot(\boldsymbol{\nabla} \times \mathbf{H}) = \boldsymbol{\nabla}\cdot\left( \mathbf{ | \boldsymbol{\nabla}\cdot(\boldsymbol{\nabla} \times \mathbf{H}) = \boldsymbol{\nabla}\cdot\left( \mathbf{J}+ \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t} \right) = 0. | ||
</math> | </math> | ||
Equation (1) is one of Maxwell's equations formulated by him in 1864 and still accepted as universally valid. The equation is in [[SI]] units; in Gaussian units it reads | Equation (1) is one of Maxwell's equations formulated by him in 1864 and still accepted as universally valid. The equation is in [[SI]] units; in Gaussian units it reads | ||
:<math> | :<math> | ||
\boldsymbol{\nabla} \times \mathbf{H}(\mathbf{r}) = \frac{4\pi}{c}\mathbf{ | \boldsymbol{\nabla} \times \mathbf{H}(\mathbf{r}) = \frac{4\pi}{c}\mathbf{J}(\mathbf{r}) + \frac{1}{c} \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t}, | ||
</math> | </math> | ||
with ''c'' the [[speed of light]]. | with ''c'' the [[speed of light]]. | ||
| Line 63: | Line 63: | ||
From | From | ||
:<math> | :<math> | ||
\boldsymbol{\nabla}\cdot\left( \mathbf{ | \boldsymbol{\nabla}\cdot\left( \mathbf{J}+ \frac{\partial\mathbf{D}(\mathbf{r})}{\partial t} \right) = 0 | ||
</math> | </math> | ||
and the divergence theorem follows | and the divergence theorem follows | ||
Revision as of 05:56, 4 July 2008
In physics, more particular in the theory of electromagnetism, the displacement current is the time derivative of the electric displacement D. It was introduced by James Clerk Maxwell as a correction to Ampère's law. It is the displacement current that gives rise to electromagnetic waves.
Explanation
In the figure on the right a capacitor (with green plates) is charged by an electric current i. The conduction current i is related to the current density J(r) by a surface integral. Since J is everywhere zero, except over the surface of the wire (blue in the figure), one may integrate over the whole closed surface of the volume V to get i,
where the last equality follows by application of the divergence theorem of Gauss. The surface integral contains the inner product between the current density J (a vector) and a vector dS orthogonal to the infinitesimal surface element dS. The orthogonal vector has length dS. The conduction current i gives the rate of change of electric charge in the volume V. Clearly, i is non-zero during the time that the capacitor is charging.
Ampère's law in differential form states that
where H(r) is the magnetic field. Since the divergence of the curl is always zero,
it follows that
at all times, in contradiction to what was just stated. Thus, Ampère's law is in error, or at least is incomplete.
Maxwell was the first to notice this and he also saw how to fix it by application of the continuity equation. This equation states that the rate of change of a charge density is proportional to the the divergence of the current density,
The electrostatic law of Gauss states
so that
So, Maxwell realized that the conduction current leaving the volume V was compensated by the displacement current entering V, which is why he added the displacement current to the conduction current density, modifying Ampère's law to
with
Equation (1) is one of Maxwell's equations formulated by him in 1864 and still accepted as universally valid. The equation is in SI units; in Gaussian units it reads
with c the speed of light.
Note
The term "displacement current" was introduced by Maxwell and is still in general use. However, the term "displacement current density" would be more appropriate. One can define the total displacement current passing through a closed surface S,
in the same way as the conduction current through the same closed surface,
From
and the divergence theorem follows
Thus, the conduction current leaving the volume enveloped by the closed surface S is equal to the total displacement current entering this volume. The displacement current shares this property with the conduction current, although there is no motion of charge involved in the former.