Clausius-Clapeyron relation

PD Image
The red line in the P-T diagram is the coexistence curve of two phases, I and II, of a single-component system. Phase I may be the vapor and II the liquid phase of the component. The lower green line gives the slope in phase I and the upper green line in phase II.

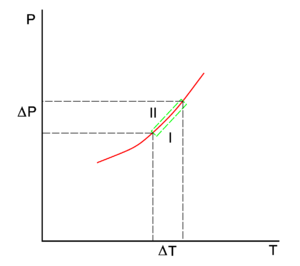
The Clausius–Clapeyron relation is an equation for a single-component system consisting of two phases in thermodynamic equilibrium at constant absolute temperature T and constant pressure P. A curve in a two-dimensional thermodynamical diagram that separates two phases in equilibrium is known as a coexistence curve. The Clausius–Clapeyron relation gives the slope of the coexistence curve in the P-T diagram:

${\frac {\mathrm {d} P}{\mathrm {d} T}}={\frac {Q}{T\,(V^{\mathrm {II} }-V^{\mathrm {I} })}},$

where Q is the molar heat of transition. It is the heat necessary to bring one mole of the compound constituting the system from phase I into phase II; it is also known as latent heat. For phase transitions with constant P, it is the molar transition enthalpy. For instance, when phase II is a liquid and phase I is a vapor, then Q ≡ H_v is the molar heat of vaporization (also known as molar enthalpy of evaporation). Further, V^I is the molar volume of phase I at the pressure P and temperature T of the point where the slope is considered and V^II is the same for phase II.

The equation is named after Émile Clapeyron, who published it in 1834, and Rudolf Clausius, who put it on firm thermodynamic basis in 1850.

Derivation

The condition of thermodynamical equilibrium at constant pressure P and constant temperature T between two phases I and II is the equality of the molar Gibbs free energies G,

$G^{\mathrm {I} }(T,P)=G^{\mathrm {II} }(T,P).\,$

The molar Gibbs free energy of phase α (α = I, II) is equal to the chemical potential μ^α of this phase. Hence the equilibrium condition can be written as,

$\mu ^{\mathrm {I} }(T,P)=\mu ^{\mathrm {II} }(T,P),\;$

which holds everywhere along the coexistence (red) curve in the figure.

If we go reversibly along the lower and upper green line in the figure [the tangents to the curve in the point (T,P)], the chemical potentials of the phases, being functions of T and P, change by Δμ^I and Δμ^II, for phase I and II, respectively, while the system stays in equilibrium,

$\mu ^{\mathrm {I} }+\Delta \mu ^{\mathrm {I} }=\mu ^{\mathrm {II} }+\Delta \mu ^{\mathrm {II} }\;\Longrightarrow \;\Delta \mu ^{\mathrm {I} }=\Delta \mu ^{\mathrm {II} }.$

From classical thermodynamics it is known that

$\Delta \mu ^{\alpha }(T,P)=\Delta G^{\alpha }(T,P)=-S^{\alpha }\Delta T+V^{\alpha }\Delta P,\quad {\hbox{where}}\quad \alpha =\mathrm {I,II} .$

Here S^α is the molar entropy (entropy per mole) of phase α and V^α is the molar volume (volume of one mole) of this phase. It follows that

$-S^{\mathrm {I} }\Delta T+V^{\mathrm {I} }\Delta P=-S^{\mathrm {II} }\Delta T+V^{\mathrm {II} }\Delta P\;\Longrightarrow \;{\frac {\Delta P}{\Delta T}}={\frac {S^{\mathrm {I} }-S^{\mathrm {II} }}{V^{\mathrm {I} }-V^{\mathrm {II} }}}.$

From the second law of thermodynamics it is known that for a reversible phase transition it holds that

$S^{\mathrm {I} }-S^{\mathrm {II} }={\frac {Q}{T}},$

where Q is the amount of heat necessary to convert one mole of compound from phase II into phase I. Elimination of the entropy and taking the limit of infinitesimally small changes in T and P gives the Clausius-Clapeyron equation,

${\frac {dP}{dT}}={\frac {Q}{T(V^{\mathrm {I} }-V^{\mathrm {II} })}}.$

Approximate solution

The Clausius-Clapeyron equation is exact. When we make the following assumptions we may perform the integration:

• The molar volume of phase I is negligible compared to the molar volume of phase II: V^II >> V^I. In general, far from the critical point, this inequality holds well for liquid-gas equilibria.

• Phase II satisfies the ideal gas law, where R is the molar gas constant,

$PV^{\mathrm {II} }=RT.\,$

If phase II is a gas and the pressure is fairly low, this assumption is reasonable.

• The transition (latent) heat Q is constant over the temperature integration interval. The integrations run from the lower temperature T₁ to the upper temperature T₂ and from P₁ to P₂.

Under these condition the Clausius-Clapeyron equation becomes

${\frac {dP}{dT}}={\frac {Q}{\frac {RT^{2}}{P}}}\;\Longrightarrow \;{\frac {dP}{P}}={\frac {Q}{R}}\;{\frac {dT}{T^{2}}}.$

Integration gives

$\int \limits _{P_{1}}^{P_{2}}{\frac {dP}{P}}={\frac {Q}{R}}\;\int \limits _{T_{1}}^{T_{2}}{\frac {dT}{T^{2}}}\;\Longrightarrow \;\ln \left({\frac {P_{2}}{P_{1}}}\right)=-{\frac {Q}{R}}\;\left({\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}\right),$

where ln(P₂/P₁) is the natural (base e) logarithm of P₂/P₁. We reiterate that for a gas-liquid equilibrium Q = H_v, the heat of vaporization.