Electromagnetic wave

In physics, an electromagnetic wave is a change, periodic in space and time, of an electric field E(r,t) and a magnetic field B(r,t). Because an electric as well as a magnetic field is involved, the term electromagnetic is used. Examples of electromagnetic waves, in increasing wavelength, are: gamma rays, X-rays, ultraviolet light, visible light, infrared, microwaves, and radio waves. All these waves propagate with the same speed c, the speed of light.

Fig. 1. Electromagnetic wave. Electric component (red) in plane of drawing; magnetic component (blue) in orthogonal plane. Wave propagates to the right. The wavelength is λ.

Details

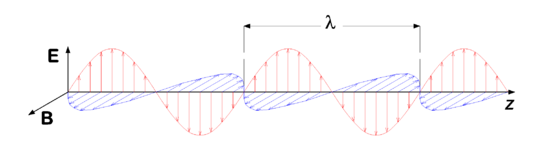
In figure 1 we see a snapshot (i.e., a picture at a certain point in time) of the magnetic and electric fields in adjacent points of space. In each point, the vector E is perpendicular to the vector B. The wave propagates to the right, along an axis which we conveniently refer to as y-axis. Both E and B are perpendicular to the propagation direction, which is expressed by stating that an electromagnetic wave is a transverse wave, in contrast to sound waves, which are longitudinal waves (i.e., air molecules vibrate parallel to the propagation direction of the sound).

Assume that the snapshot in figure 1 is taken at time t, then at a certain point y we see an arrow of certain length representing E(y,t) and also a vector B(y,t). At a point in time Δt later, the same values of E and B (same arrows) are seen at y + c Δt. The arrows seem to have propagated to the right with a speed c.

Fig. 2. Schematic overview of electromagnetic spectrum. Vertical axis: wavelengths in meter. Examples: infrared extends from 8 ·10⁻⁷ to 10⁻³ m; radio from 10⁻⁴ to about 10⁴ m.

In figure 1, the time t is fixed and the position y varies. Conversely, we can keep the position fixed and imagine what happens if time changes. Focus on a fixed point y, then in progressing time the two vectors E(y,t) and B(y,t) in the point y, grow to a maximum value, then shrink to zero, become negative, go to a minimum value, and grow again, passing through zero, they grow to the same maximum value again. This cycle is repeated indefinitely. When we now plot E and B in the fixed point y as a function of time t, we see the same type (sine-type) function as in figure 1. The number of times per second that the vectors go through a full cycle is the frequency of the electromagnetic wave.

Periodicity in space means that the electromagnetic (EM) wave is repeated after a certain distance. This distance, the wavelength is traditionally designated by λ, see figure 1. If we go at a fixed time a distance λ to the right or to the left we encounter the very same fields E and B.

Basically, the only property distinguishing different kinds of EM waves, is their wavelength, see figure 2. Note the enormous span in wavelengths, from one trillionth of a millimeter for gamma-rays (radioactive rays) up to the VLF (very low frequency) radiowaves of about 100 kilometer.

Often EM waves are characterized by their frequency. If the EM field goes through ν full cycles in a second, where ν is a positive integral number, we say that the field has a frequency of ν Hz (hertz). In 1/ν of a second the wave has propagated c/ν m, which is the wavelength λ:

$\lambda ={\frac {c}{\nu }}\quad \Longrightarrow \quad \nu ={\frac {c}{\lambda }}$

If we express c in m/s then λ is obtained in meters. To convert from wavelength to frequency we can approximate c by 3·10⁸ m/s. Thus, for instance,

λ = 3·10⁻¹⁰ m → ν = 10¹⁸ Hz (X-ray)

λ = 3·10⁻² m  → ν = 10¹⁰ Hz = 10GHz (Microwave)

λ = 3·10² m   → ν = 10⁶ Hz = 1 MHz (Radiowave)

Relation to Maxwell's equations

To be continued

External link

ISO 21348 Definitions of Solar Irradiance Spectral Categories

To be continued