Surface-based morphometry
In neuroimaging, surface-based morphometry (often abbreviated SBM) is a group of brain morphometric techniques used to construct and analyze surfaces that represent structural boundaries of the brain. One example is the boundary between white and grey matter of the cerebral cortex, often referred to as the white matter surface.
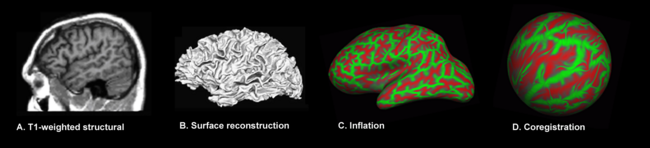
The major steps involved in surface-based morphometry of the brain: Image acquisition, surface reconstruction, surface inflation (green representing gyral regions, red sulcal ones) and surface mapping. The transition from A to B requires a set of preprocessing steps whose major elements are shared with voxel- and deformation-based morphometry: image registration, intensity normalization, smoothing, brain extraction and brain segmentation.
These boundaries are defined by or on the basis of a brain segmentation, and the surface is generated by a meshing algorithm (e.g. marching cubes) that codifies relationships between voxels on the boundary into relationships between polygonal or polyhedral surface elements.
This does not require registering the individual brain images to a template brain, though comparisons across brains demand a reference surface that belongs to the same topological genus (i.e. 0) and is normalized in size. The brains are thus mapped to a unit sphere on which their original properties can be compared with each other, and results are mapped back to a reference brain surface.
The surfaces most appropriate for cortical analyses are the boundaries between white and grey matter or between grey matter and cerebrospinal fluid (the latter surface is also often referred to as pial surface, since the pia mater is not commonly segmented into a class of its own) but various representations of the so-called central surface (roughly corresponding to the anatomical lamina IV) are also in use. For some subcortical structures (e.g. the hippocampus or basal ganglia), appropriate surfaces can be defined in a similar way, while lateral delineation of the corpus callosum, for instance, is difficult.
Statistical analyses in surface-based morphometry are based on properties of the individual mesh elements and aggregations thereof. These latter ones include, foremostly, some measure of the distance between different surfaces-- typically the cortical thickness-- or sulcal depth but also some local or global measures of area, curvature (e.g. gyrification) or overall shape (e.g. via spherical wavelets, spherical harmonics or Laplace-Beltrami spectra).