Transition element

A transition element is a chemical element whose atomic electron configuration of the ground (lowest energy) state has an incompletely filled d sub-shell. Table I shows the part of the Periodic Table that contains the first three series of transition elements. The symbol "d" stands for an atomic orbital with angular momentum quantum number ℓ = 2. The electron configuration of transition element atoms contains (nd)^k, 1 ≤ k ≤ 9, where n is a principal quantum number, n = 3, 4, 5, see Table II. The incomplete electronic d subshell gives rise to some characteristic magnetic properties (paramagnetism and ferromagnetism) and crystals and solutions of transition metal complexes that are brightly colored.

The elements in the fourth transition series (period 7 of the periodic table), are formally transition elements. They are man-made [except for Actinium (Z = 87)] and short-lived, not much is known about their compounds and accordingly they are not discussed in this article.

I. Rows and columns of the Periodic Table of Elements containing transition elements The atomic number Z is between brackets Group 3 4 5 6 7 8 9 10 11 1st series Sc (21) Ti (22) V (23) Cr (24) Mn (25) Fe (26) Co (27) Ni (28) Cu (29) 2nd series Y (39) Zr (40) Nb (41) Mo (42) Tc (43) Ru (44) Rh (45) Pd (46) Ag (47) 3rd series La (57) Hf (72) Ta (73) W (74) Re (75) Os (76) Ir (77) Pt (78) Au (79)

Exceptions to the definition

Although the atoms copper (Cu), silver (Ag), and gold (Au) have a filled d sub-shell in their lowest energy state—as Table II shows they have the configuration (nd)¹⁰(n+1)s¹, with n = 3, 4, and 5, respectively—after ionization (loss of two or more electrons) their cations have an incomplete d sub-shell. Since these cations appear in many complexes, copper, silver, and gold are usually seen as transition elements.

II. Electron Configurations Z Symbol Element Core Configuration 21 Sc Scandium  [Ar] (3d)1 (4s)2 22 Ti Titanium  [Ar] (3d)2 (4s)2 23 V Vanadium  [Ar] (3d)3 (4s)2 24 Cr Chromium  [Ar] (3d)5 (4s)1 25 Mn Manganese  [Ar] (3d)5 (4s)2 26 Fe Iron  [Ar] (3d)6 (4s)2 27 Co Cobalt  [Ar] (3d)7 (4s)2 28 Ni Nickel  [Ar] (3d)8 (4s)2 29 Cu Copper  [Ar] (3d)10(4s)1 39 Y Yttrium  [Kr] (4d)1 (5s)2 40 Zr Zirconium  [Kr] (4d)2 (5s)2 41 Nb Niobium  [Kr] (4d)4 (5s)1 42 Mo Molybdenum  [Kr] (4d)5 (5s)1 43 Tc Technetium  [Kr] (4d)5 (5s)2 44 Ru Ruthenium  [Kr] (4d)7 (5s)1 45 Rh Rhodium  [Kr] (4d)8 (5s)1 46 Pd Palladium  [Kr] (4d)10 47 Ag Silver  [Kr] (4d)10(5s)1 57 La Lanthanum  [Xe] (5d)1 (6s)2 72 Hf Hafnium [Xe*] (5d)2 (6s)2 73 Ta Tantalum [Xe*] (5d)3 (6s)2 74 W Tungsten [Xe*] (5d)4 (6s)2 75 Re Rhenium [Xe*] (5d)5 (6s)2 76 Os Osmium [Xe*] (5d)6 (6s)2 77 Ir Iridium [Xe*] (5d)7 (6s)2 78 Pt Platinum [Xe*] (5d)9 (6s)1 79 Au Gold [Xe*] (5d)10(6s)1 [Ar] stands for:   (1s)2(2s)2(2p)6 (3s)2(3p)6 [18] [Kr] stands for:   [Ar](3d)10(4s)2(4p)6 [36] [Xe] stands for:   [Kr](4d)10(5s)2(5p)6 [54] [Xe*] stands for:   [Xe](4f)14 [68]

In the past, the group 12 elements zinc (Zn), cadmium (Cd), and mercury (Hg), that are included in the "d-block" of the periodic table, have been considered as transition elements, but they are nowadays rarely considered as such, because their compounds lack some of the properties that are characteristic for transition elements.

Because scandium (Sc), yttrium (Y), and lanthanum (La) actually do not form compounds analogous to those of the other transition elements and because their chemistry is quite homologous to that of the lanthanoids (previously known as lanthanides), they are often excluded from the group of transition elements. A strict application of the definition would describe also lutetium (Lu) as a transition element as it has a singly occupied 5d orbital in its ground state, but according to IUPAC it is a lanthanoid. Lutetium appears most commonly as a positive ion without d-electrons in the valence shell and without the characteristic properties of a transition element.

Properties

The most striking similarities shared by the transition elements is that they are all metals—which is why they are often called transition metals—and that most of them are hard, strong, and shiny. They have high melting and boiling points, and, being metals, are good conductors of heat and electricity. Many of the elements are technologically important: iron, nickel, cobalt, palladium, platinum, and others are used in heterogeneous catalysis. Much of the current research on the chemistry of transition element complexes is instigated by their industrial importance as catalysts.

The transition elements form many useful alloys, among themselves and with other metallic elements. Most of the transition elements can be dissolved in water and other polar solvents and form complexes in solution, although the "noble" metals platinum, silver, and gold are difficult to dissolve. For obvious reasons the elements copper, silver, and gold are referred to as coinage metals. Note that copper belongs to the class of coinage metals, but is not a noble metal.

The outer s-electrons of the transition metals are easily lost to the bonding partners (the ligands) of the metal. Also one or more d-electrons of the metal are usually lost to its ligands. In other words, most transition element compounds show ionic chemical bonds. Common ligands are: oxide (O²⁻), halides (F⁻, Cl⁻, Br⁻, I⁻), hydrates (H₂O, OH⁻), cyanide (CN⁻), and sulfate (SO₄²⁻).

The formal charge of the ionically bound element is known as its oxidation number, or oxidation state. Table III shows the most common oxidation states of the first transition series. Note in this table that the elements exhibit variable oxidation states. The chemistry of the transition series is mainly that of the ions in one of their several oxidation states, and not that of the elemental form itself.

For example, the transition element chromium (Cr) in the ionic water complex chromium hexahydrate, Cr(H₂O)₆³⁺, is trivalent and is denoted by the oxidation state Cr(III). (This is because water has formal oxidation number zero.) The very commonly occurring Cr(III) cation has electronic structure [Ar](3d)³; it appears, for instance, also in the crystal KCr(SO₄)₂⋅(H₂O)₁₂. The chromium in Cr(CN)₆⁴⁻ is divalent, denoted by Cr(II); it has electronic structure [Ar](3d)⁴. Chromate [CrO₄]²⁻ contains Cr(VI), which is isoelectronic with argon. An example of monovalent Cr(I) is the bright-green compound K₃[Cr(CN)₅NO]⋅H₂O, which contains K⁺, Cr⁺, NO⁺, and CN⁻.

This widely applied classification of transition elements by their oxidation states is not supported by quantum mechanical calculations. Although many theoretical discussions of transition metal complexes assume (often implicitly) ionic bonds, quantum mechanical calculations show that most of the bonds have a good deal of covalent character. Calculations bear out that transfer of more than one full electron to the ligands occurs rarely, let alone six electrons as in Cr(VI). However, in qualitative and semi-quantitative studies, the assumption of ionic bonds with a transition metal cation, provides much insight and yields a systematization of the properties of the transition metal complexes. The covalent character of the bonds is accounted for by the values of the semi-empirical parameters that enter such studies.

III. Oxidation states of first series Red entries: Most common occurrence. Blue entries: common occurrence. Sc Ti V Cr Mn Fe Co Ni Cu       I(d5 )         I(d10) II(d1 ) II(d2 ) II(d3 ) II(d4 ) II(d5 ) II(d6 ) II(d7 ) II(d8 ) II(d9 ) III(d0 ) III(d1 ) III(d2 ) III(d3 ) III(d4 ) III(d5 ) III(d6 ) III(d7 ) III(d8 )   IV(d0) IV(d1) IV(d2 ) IV(d3 ) IV(d4 ) IV(d5 ) IV(d6 )     V(d0 ) V(d1 ) V(d2 ) V(d3 ) V(d4 )           VI(d0 ) VI(d1 ) VI(d2 )               VII(d0 )

Quantum mechanical description

In a landmark paper Hans Bethe introduced in 1929 a model known as the crystal field model. This model successfully accounts for some magnetic properties and colors of transition metal complexes. It describes a transition metal ion in an electrostatic field created by the surrounding charged or dipolar ligands. The electrostatic field has point group symmetry lower than the full rotation symmetry SO(3) of the free atom. Because of the symmetry lowering the (2S+1)(2L+1) different functions that are degenerate in the free atom (a so-called "term" represented by a term symbol) will split up, that is, will obtain different energies. Because the crystal field is non-magnetic, the spin S will be conserved. However, the atomic orbital momentum L will be quenched, i.e., inside the crystal field angular momentum is not conserved, L is no longer a good quantum number.

The crystal field model does not attempt to describe why the configuration of atoms and surrounding ligands is stable. After 1929 the crystal field model was extended by the admixture of ligand orbitals into the atomic orbitals of the central ion. This extended model is known as the ligand field model. The ligand field model aims at predicting correct binding energies in addition to the explanation of magnetic and spectral properties.

PD Image
Transition metal ion (red) in octahedron of ligands(black). The ligands are in the centers of the faces of the cube.

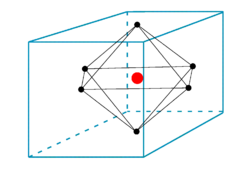
In order to give the flavor of the crystal field model, we consider the simplest case: one electron in an electric field of octahedral symmetry. An example is the ion [Ti(H₂O)₆]³⁺.

Octahedral potential

In the figure we see six ligands in the centers of the six faces of a cube. The field inside the cube created by the ligands (that are either charged or dipolar), satisfies the Laplace equation

$\nabla ^{2}V(r,\theta ,\phi )=0,$

where r, θ, and φ are spherical polar coordinates of a point with respect to a system of axes centered on the central ion. It is known that the regular solid harmonics R^m_ℓ form a solution of the Laplace equation. Hence, the following expansion is exact

$V(r,\theta ,\phi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\;A_{\ell ,m}R_{\ell }^{m}(r,\theta ,\phi ).$

In quantum mechanics a symmetry operation, such as a rotation around an axis, reflection in a plane, or inversion in a point, is defined as an operation that leaves invariant (commutes with) the energy (Hamilton) operator of the system. Here we turn the argument around and adapt the expansion of the potential field to the octahedral symmetry in order that the expansion becomes invariant under the octahedral symmetry operations.

One of the octahedral symmetry operations is inversion with respect to the origin (the position of the metal ion). It is known that regular harmonics are mapped onto themselves multiplied by a factor (−1)^ℓ by inversion. In other words, only terms with even ℓ will appear in the expansion of V. The function for ℓ = m = 0 is simply unity, the constant function of value one.

As first shown by Bethe by means of group theoretical character relations, there are no linear combinations of the five d-type functions that span the totally symmetric representation of the octahedral group—no linear combinations can be found that are invariant . Hence the first ℓ that can contribute has value ℓ = 4. Also higher ℓ-values can give totally symmetric octahedral functions, but we will see below that in the example at hand (a single d-electron inside the cube) they will not contribute. It can be shown that the following function is the only totally invariant function of ℓ = 4:

$V_{4}(r,\theta ,\phi )\equiv {\sqrt {14}}\,R_{4}^{0}+{\sqrt {5}}\,(R_{4}^{4}+R_{4}^{-4}).$

The octahedral potential becomes (truncated at ℓ = 4):

$V_{\mathrm {oct} }(r,\theta ,\phi )=A+B\,V_{4}(r,\theta ,\phi )\,$

where the constants A and B may be used as fit parameters.

First order perturbation theory

The free ion is in a five-fold degenerate state with term symbol ²D, i.e., the electron can be in any of the five d-orbitals. The ion is perturbed by the crystal field. If this field is weak, first-order perturbation theory suffices. This means that we have to set up the perturbation matrix of V on basis of the five d-orbitals,

$\mathbf {V} ={\begin{pmatrix}\langle d_{-2}\;|\;V_{\mathrm {oct} }\;|\;d_{-2}\rangle &\langle d_{-2}\;|\;V_{\mathrm {oct} }\;|\;d_{-1}\rangle &\langle d_{-2}\;|\;V_{\mathrm {oct} }\;|\;d_{0}\rangle &\langle d_{-2}\;|\;V_{\mathrm {oct} }\;|\;d_{1}\rangle &\langle d_{-2}\;|\;V_{\mathrm {oct} }\;|\;d_{2}\rangle \\\langle d_{-1}\;|\;V_{\mathrm {oct} }\;|\;d_{-2}\rangle &\langle d_{-1}\;|\;V_{\mathrm {oct} }\;|\;d_{-1}\rangle &\langle d_{-1}\;|\;V_{\mathrm {oct} }\;|\;d_{0}\rangle &\langle d_{-1}\;|\;V_{\mathrm {oct} }\;|\;d_{1}\rangle &\langle d_{-1}\;|\;V_{\mathrm {oct} }\;|\;d_{2}\rangle \\\langle d_{0}\;|\;V_{\mathrm {oct} }\;|\;d_{-2}\rangle &\langle d_{0}\;|\;V_{\mathrm {oct} }\;|\;d_{-1}\rangle &\langle d_{0}\;|\;V_{\mathrm {oct} }\;|\;d_{0}\rangle &\langle d_{0}\;|\;V_{\mathrm {oct} }\;|\;d_{1}\rangle &\langle d_{0}\;|\;V_{\mathrm {oct} }\;|\;d_{2}\rangle \\\langle d_{1}\;|\;V_{\mathrm {oct} }\;|\;d_{-2}\rangle &\langle d_{1}\;|\;V_{\mathrm {oct} }\;|\;d_{-1}\rangle &\langle d_{1}\;|\;V_{\mathrm {oct} }\;|\;d_{0}\rangle &\langle d_{1}\;|\;V_{\mathrm {oct} }\;|\;d_{1}\rangle &\langle d_{1}\;|\;V_{\mathrm {oct} }\;|\;d_{2}\rangle \\\langle d_{2}\;|\;V_{\mathrm {oct} }\;|\;d_{-2}\rangle &\langle d_{2}\;|\;V_{\mathrm {oct} }\;|\;d_{-1}\rangle &\langle d_{2}\;|\;V_{\mathrm {oct} }\;|\;d_{0}\rangle &\langle d_{2}\;|\;V_{\mathrm {oct} }\;|\;d_{1}\rangle &\langle d_{2}\;|\;V_{\mathrm {oct} }\;|\;d_{2}\rangle \\\end{pmatrix}}.$

The angular part of the d_m orbital is the spherical harmonic Y^m_ℓ.

According to perturbation theory we must diagonalize the matrix V (find its eigenvalues and eigenvectors). Nowadays, in the era of computers, it is easy to diagonalize this matrix numerically. In the days of Bethe this was not possible, so that he was forced to find linear combinations of the d-orbitals with well-defined symmetry properties (technically: linear combinations that span irreducible representations of the octahedral group). Bethe found that there are 3 + 2 combinations, which we do not need explicitly, but symbolically are

$\{|t_{2g},1\rangle ,\quad |t_{2g},2\rangle ,\quad |t_{2g},3\rangle \}\quad {\hbox{and}}\quad \{|e_{g},1\rangle ,\quad |e_{g},2\rangle \}$

The first three span the 3-dimensional irreducible representation T_2g and the second two the 2-dimensional irreducible representation E_g. Just as the original d_m orbitals, the functions are orthonormal, that is, the transformation between the two sets is orthogonal. Group theory shows that

$\langle t_{2g},i\;|\;V_{\mathrm {oct} }\;|\;t_{2g},j\rangle =\delta _{ij}(A+X)\qquad \langle e_{g},i\;|\;V_{\mathrm {oct} }\;|\;e_{g},j\rangle =\delta _{ij}(A+Y)\quad {\hbox{and}}\quad \langle t_{2g},i\;|\;V_{\mathrm {oct} }\;|\;e_{g},j\rangle =0,$

where X and Y are proportional to the potential parameter B. Transformation of V to a basis of these group theoretically determined functions gives the matrix the following diagonal form

$\mathbf {V} \rightarrow {\begin{pmatrix}A+X&0&0&0&0\\0&A+X&0&0&0\\0&0&A+X&0&0\\0&0&0&A+Y&0\\0&0&0&0&A+Y\\\end{pmatrix}}.$

Because this matrix is diagonal it means that we have found the eigenvalues (the diagonal elements) and the eigenvectors (the group theoretical functions). The first eigenvalue (energy of the state of T_2g symmetry) is 3-fold degenerate and the energy of the state of E_g is 2-fold degenerate. The energy difference between the two states is (A+ Y) −(A+ X) = Y − X ≡ 10Dq. The notation 10Dq is traditional.

Since the octahedral potential consists of regular solid harmonics we may apply the Wigner-Eckart theorem

$\langle d_{m}\;|\;R_{\ell }^{\mu }\;|\;d_{m}\rangle =C\,(-1)^{m}{\begin{pmatrix}2&\ell &2\\-m&\mu &m\end{pmatrix}}$

where the quantity between round brackets is a Wigner 3j-symbol and C is a constant independent of m and μ. Because the 3j-symbol is zero whenever ℓ > 4, it follows that higher than ℓ = 4 potential terms do not contribute in first-order of perturbation theory.

Trace of perturbation matrix

The trace of the perturbation matrix is

$\mathrm {Tr} (\mathbf {V} )=\sum _{m=-2}^{2}\langle d_{m}\;|\;V_{\mathrm {oct} }\;|\;d_{m}\rangle$

Since

$\sum _{m=-2}^{2}(-1)^{m}{\begin{pmatrix}2&\ell &2\\-m&\mu &m\end{pmatrix}}=C\,{\sqrt {5}}\,\delta _{\ell ,0}\,\delta _{m,0}$

it follows that V₄ does not contribute to the trace (it consist of ℓ = 4 terms only). Now,

$\mathrm {Tr} (\mathbf {V} )=\sum _{m=-2}^{2}\langle d_{m}\;|A\;|\;d_{m}\rangle =5A.$

The trace of the original matrix is equal to the trace of the diagonal matrix, because the two matrices are connected by a orthogonal transformation. Hence

$5A+3X+2Y=5A\quad {\hbox{and}}\quad Y-X=10\mathrm {Dq} \Longrightarrow X=-4\mathrm {Dq} ,\;Y=6\mathrm {Dq} .$

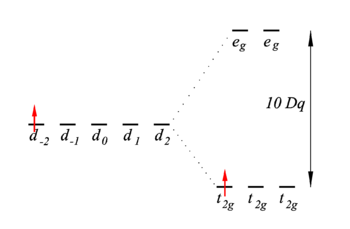
Energy level scheme

PD Image
Energy levels of a one-electron ion in an octahedral field. The electron (red arrow) is drawn in one orbital, but in reality is with equal probability in all the orbitals of the same energy.

The first-order energies (eigenvalues of V) are shown in the figure on the right. The t_2g energies are shifted down over a distance 4Dq and the e_g energies are shifted up by 6Dq.

The two most important conclusions are:

• There is one unpaired electron in the lowest energy state. This means that the complex is paramagnetic, the unpaired electron will align in a magnetic field.
• An excitation from t_2g to e_g is possible. The excitation energy is equal to 10Dq. Typically the value of 10Dq is around 20 000 cm⁻¹, or 500 nm. This is in the visible region of the electromagnetic spectrum and explains the color of the complex.

Finally, it must be pointed out that strictly speaking the t_2g to e_g transition is forbidden under the usual dipole operator associated with the electromagnetic field. This is because the dipole is ungerade (odd) under inversion and the states are gerade (even, hence the subscripts g.) A quadrupole transition would be allowed but is much to weak. It turns out that the transition is allowed because of vibronic coupling. This means that the Born-Oppenheimer approximation is not strictly valid, the vibration of the nuclei and the electron is coupled (hence the name "vibronic"). In the Born-Oppenheimer approximation it is assumed that the motions are completely uncoupled.