Fourier operator
Fourier operator is linear integral operator with the exponential kernel.
Let some complex–valued function be defined for real values of the argument, id est, . Then the Fourier operator, acting on , gives function , or, simply, , such that
If the integral converges, then, function is called Fourier transform of function .
Other notations
Slightly different notations are used in the article Fourier transform; operator is defined such that
In such a way,
Inverse operator
The inverse of the Fourier operator is its conjugate, id est,
where acts on a function in such a way, that
Then, for the operator , the inverse acts on a fiction as follows:
Application of the Fourier operator
The Fourier transform is used in various sciences and, especially, in physics. In Quantum mechanics, function may have sense of the wave function in the coordinate representation, then corresponds to the momentum representation. Many equations can be solved using the Fourier Transform. Especially efficient is the Fourier transform in the consideration of the paraxial approximation of the wave equations.
General properties of the Fourier operator
The Fourier operator is linear: for complex constants and ,
Norm of the Fourier operator
The norm of a function can be defined as
The norm of any function is assumed to be non–negative; .
The Fourier operator is unitary, so, it preserves the norm of a function; if then
Iteration of the Fourier operator
The iterations of the Fourier operator do not provide a wide variety, because
Any integrable continuous function can be used as a an origin to construct a self–Fourier function as a polynomial
which is self-Fourier function; id set, $~S~$ is eigenfunction of the Fourier operator with eigenvalue unity.
Self–Fourier functions
In general, function is called self-Fourier function, if
All the self-Fourier functions are eigenfunction of the Fourier operator with eigenvalue unity. Any self–Fourier function can be represented as series,
where are the Hermit polynomials [1], and are arbitrary complex coefficients; the sequence should decay quickly enough to provide the convergence of the series [2].
In particular, the first three self-Fourier functions can be defined with
The self-Fourier functions are good for testing of the numerical implementations of the Fourier operator .
Numerical implementation of the Fourier operator
In order to approximate the Fourier operator, the Discrete Fourier operator is used. In this section, the numerical implementation is discussed. The C++ implementation fafo.cin of operator $\mathrm{Fourier}$ is used to plot figures. This implementation is described below. The codes used to plot figures are supplied in the descriptions of the figures.
There is no need to describe functions , , and so on separately, it is sufficient to have function sin. In the similar way, it is sufficient to describe the discrete implementation of the Fourier operator at some grid. Then, other implementations can be built-up with minimal modifications of the algorithm, shifting and scaling the argument of the function and applying the corresponding modifications to the Fourier transform.
For the number of grid points, the step of the grid is chosen as follows:
The grid points , are chosen for natural number ; in the following way:
At such a discretization, the node with number always corresponds to the argument zero. The 0th node is assumed to be at the left hand side of the sampled range. However, it can be placed also at the right hand side as well, and interpreted as $x_{N}$. The algorithm makes no difference between these points.
The same grid is used both for the function and for its Fourier–transform. Functions and are represented with the arrays;
The approximation of corresponds to the replacement of the integral to the discrete sum:
It is convenient to chose for some natural number ; then the fast implementation of such a summation is especially simple.
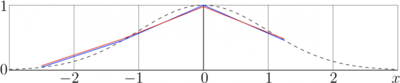
For the testing of the algorithm, the transform of discrete analogy of the Gaussian exponential is suggested at the figure above.
Such a Gaussian is self-Fourier function, and it coincides with its Fourier-transform. However, at small number of the grid points, , the deviation of the blue segmented line (that represents the array ) deviates from the red line, that represents the array as the numeric transform of . At larger number of grid points, the strong zooming-in is necessary to see the deviation. Similar example with is considered in the article fast Fourier transform; however, for the Gaussian self-Fourier function, at the deviation of the numerical evaluation of the Fourier operator from the initial function is very small and is not seen at the figures.
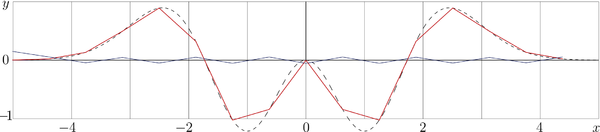
A little bit more complicated example with self-Fourier function
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\displaystyle (20) ~ ~ ~ A(x)\!=\!\exp(-x^2/2)(−3x^2+x^4)}
is shown in figure at right in the same notations, as in previous figure, but . In this case, the segmented lines for arrays and overlap so perfectly, that the deviation is not seen. This deviation scaled with factor 100 is shown with the saw-like line along the abscissa axis. The deviation is of order of , and only in the 0th node of the grid it is a little bit larger, than .
The examples show, that the numerical approximation of the Fourier operator is much better, than the 1st order approximation of the function and its Fourier transform with the arrays and , the deviation of the segmented line from the smooth Gaussian is much larger than the deviation of the initial array from its discrete transform.
Everyone may load the code and play with the discrete implementation of the Fourier operator for various input arrays, approximating various functions.
Keywords
Fourier, Integral transform, Linear algebra
References
- ↑ http://mathworld.wolfram.com/HermitePolynomial.html
- ↑ http://www.tandfonline.com/doi/abs/10.1080/09500349908231393#preview R.Ortega, C.J.Román, D.Kouznetsov. On the second order characterization of ultrashort pulses. Journal of Modern Optics, v.46, No.15, p.2069-2077 (1999).
http://mathworld.wolfram.com/FourierTransform.html
The content of this article is adopted from http://tori.ils.uec.ac.jp/TORI/index.php/Fourier_operator