Logistic sequence

Iterations of the logistic transfer function, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_4^c(x)} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=} 0.2, 0.5, 0.8,1, 1.2, 1.5

Logistic sequence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_u} is Superfunction of the quadratic transfer function

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_u(z)=u~ z ~ (1\!-\!z)}

Parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} is usually assumed to be a positive constant. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u>1} , the logistic sequence is entire function; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_u(z) \approx u^z+\mathcal O(u^{2z})} as the real part of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} approaches to minus infinity.

The transfer function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} is called also logistic operator. The non-integer iterates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} can be expressed through the logistic sequence and its inverse function.

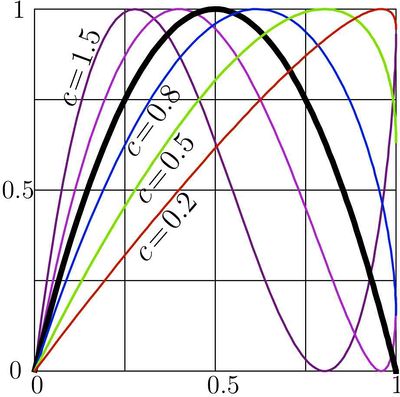
For the special case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=4} , the logistic sequence can be expressed in terms of elementary functions; for this case, the iterations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_4^c(x)} are plotted versus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=} 0.2, 0.5, 0.8, 1, 1.2, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.5} In figure at right.

Evaluation of the logistic sequence

The non-integer iterations of the logistic operator can be constructed using the analytic continuation of the logistic sequence. The logistic sequence is function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} satisfying the recurrent equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z\!+\!1)=f_u(F(z))}

Initially, such an equation was considered for integer values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} , see, for example, , but then it was generalized for complex values . In the simplest case, the logistic sequence allow the asymptotic representation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z)= u^z+ a_2 u^{2z} + a_3 u^{3z}+a_4 u^{4z}+...}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_2} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_3} , .. are real coefficients. These coefficients can be found at the substitution of the asymptotic representation to the recurrent equation. In particular,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_2=\frac{-1}{u-1}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_3=\frac{2}{(u-1)(u^2-1)}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_4=\frac{-5-u}{(u-1)(u^2-1)(u^3-1)}}

With some Maple or Mathematica, one can easy calculate a dozen of such coefficients. More complicated solutions with other asymptotic behaviors can be constructed in the similar way.

The series above diferge, but still allow the fast and precise evaluation. For value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^z} is not small, the asymptotic representation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z)=f_u^n(z\!-\!n)}

can be used for some natural Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^{z-n}} is small.

Inverse of the logistic sequence

For the logistic transfer function, the Abel function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} is the inverse function of the logistic sequence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} . The Abel function satisfies the Abel equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(f(z))=G(z)+1}

This Abel-function can be expressed through the asimptotic representation, inverting that for the Superfunciton:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(z)=\log_u(z+s_2 z^2+s_3 z^3+...)}

The coefficients Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} can be found substituting the representation into the Abel equation; with some Mathematica of Maple one can easy get a dozen of such coefficients. In particular,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_2=-a_2=\frac{1}{u-1}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_3=\frac{2u}{ (u-1)(u^2-1) }}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_4=\frac{(u^2-5)u}{(u-1)(u^2-1)(u^3-1)}}

Again, the series is asymptotic, and if the argument is not small, the Abel function can be evaluated as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(z)=F(f^{-n}(z))+n}

for some natural </math>n</math> such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f^{-n}(z)|\ll 1} .

The inverse function for the logistic operator can be expressed as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{-1}(z)= \frac{1}{2} - \sqrt{\frac{1}{4}-\frac{z}{u}}}

Iterations of the logistic operator

As usually, the combination of the superfunction (which is logistic sequence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} ) and the Abel function (which is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} , the inverse of the logistic sequence) allows to evaluate the arbitrary (in particular, fractional and even complex) iterations of the logistic transfer function:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^c(z)=F(c+G(z))}

This representation is used to plot the non-integer iterates of the logistic operator, shown in the upper right corner of this article. Namely for the case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=4} , the representation through the elementary function could be used too. Such a representation is described below.

Special case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=4}

The logistic sequence is relatively simple superfunction, and in the case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u\!=\!4} , it can be expressed through the elementary function,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z)=\frac{1}{2}(1-\cos(2^z))}

In this case, the Abel function

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(z)=\log_2(\arccos(1-2z))}

Such a representation follows also from the table of superfunctions .

The combination gives the expression for the iteration of the transfer function:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^c(z)=\frac{1}{2} \Big(1-\cos\Big(\exp_2(c+\log_2(\arccos(1-2z)) \Big)\Big) }

Such a representation can be simplified, this leads to the expression

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^c(z)=\frac{1}{2} \Big(1-\cos\Big(2^c~\arccos(1-2z) \Big)\Big) }

In such a way, for $u\!=\!1$, the iterations of the logistic operator, as well as its Superfunction and the Abelfunction can be expressed through the elementary functions. The last expression could be obtained also using the Schroeder function of the logistic operator.

Conclusion

For values $u>1$, the logistic sequence $F_{u}$ appears as superfunction of the logistic operator $f_{u}$. Together with the Abel function $G_{u}$, this allows to evaluate various iterates of the logistic operator. In particular, the square root of the logistic operator can be evaluated, id est, such function $h$ that $h(h(z))=f(z)$.

In the similar way, the superfunctions and the Abel functions can be evaluated for various transfer functions. One may evaluate the square root of factorial (used as logo of the Physics Department of the MSU and as part of the logo of TORI ), and also the ${\sqrt {\exp }}$, discussed in , and various superfunctions, including the Ackermann functions.

This article had been copypasted and adopted (in particular, <\nowiki> $...$ were replaced to $...$</nowiki>) from .