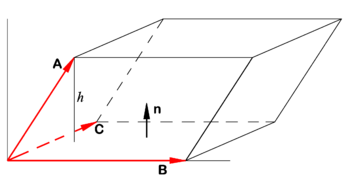
CC Image Parallelepiped spanned by vectors
A,
B, and
C (shown in red).
In analytic geometry, a triple product is a common term for a product of three vectors A, B, and C leading to a scalar (a number). The absolute value of this scalar is the volume V of the parallelepiped spanned by the three vectors:

where B × C is the cross product of two vectors (resulting into a vector) and the dot indicates the inner product between two vectors (a scalar).
The triple product is sometimes called the scalar triple product to distinguish it from the vector triple product A×(B×C). The scalar triple product is often written as [A B C]. The vector triple product can be expanded by the aid of the baccab formula.
Explanation
Let n be a unit normal to the parallelogram spanned by B and C (see figure). Let h be the height of the terminal point of the vector A above the base of the parallelepiped. Recall:
- Volume V of parallelepiped is height h times area S of the base.
Note that h is the projection of A on n and that the area S is the length of the cross product of the vectors spanning the base,

Use

where it is used that

(The unit normal n has the direction of the cross product B × C).
If A, B, and C do not form a right-handed system, A•n < 0 and we must take the absolute value: | A• (B×C)|.
Triple product as determinant
Take three orthogonal unit vectors i , j, and k and write

The triple product is equal to a 3 × 3 determinant

Indeed, writing the cross product as a determinant we find
![{\displaystyle {\begin{aligned}\mathbf {A} \cdot (\mathbf {B} \times \mathbf {C} )&=\mathbf {A} \cdot {\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\B_{1}&B_{2}&B_{3}\\C_{1}&C_{2}&C_{3}\\\end{vmatrix}}\\&={\big (}A_{1}\mathbf {i} +A_{2}\mathbf {j} +A_{3}\mathbf {k} {\big )}\cdot {\big [}(B_{2}\,C_{3}-B_{3}\,C_{2})\;\mathbf {i} +(B_{3}\,C_{1}-B_{1}\,C_{3})\;\mathbf {j} +(B_{1}\,C_{2}-B_{2}\,C_{1})\;\mathbf {k} {\big ]}\\&=A_{1}\;(B_{2}\,C_{3}-B_{3}\,C_{2})+A_{2}\;(B_{3}\,C_{1}-B_{1}\,C_{3})+A_{3}\;(B_{1}\,C_{2}-B_{2}\,C_{1})\\&={\begin{vmatrix}A_{1}&A_{2}&A_{3}\\B_{1}&B_{2}&B_{3}\\C_{1}&C_{2}&C_{3}\\\end{vmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d7af0616ddf13297024357fc90e030e39b4534)
Since a determinant is invariant under cyclic permutation of its rows, it follows

Reference
M. R. Spiegel, Theory and Problems of Vector Analysis, Schaum Publishing, New York (1959) p. 26







![{\displaystyle {\begin{aligned}\mathbf {A} \cdot (\mathbf {B} \times \mathbf {C} )&=\mathbf {A} \cdot {\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\B_{1}&B_{2}&B_{3}\\C_{1}&C_{2}&C_{3}\\\end{vmatrix}}\\&={\big (}A_{1}\mathbf {i} +A_{2}\mathbf {j} +A_{3}\mathbf {k} {\big )}\cdot {\big [}(B_{2}\,C_{3}-B_{3}\,C_{2})\;\mathbf {i} +(B_{3}\,C_{1}-B_{1}\,C_{3})\;\mathbf {j} +(B_{1}\,C_{2}-B_{2}\,C_{1})\;\mathbf {k} {\big ]}\\&=A_{1}\;(B_{2}\,C_{3}-B_{3}\,C_{2})+A_{2}\;(B_{3}\,C_{1}-B_{1}\,C_{3})+A_{3}\;(B_{1}\,C_{2}-B_{2}\,C_{1})\\&={\begin{vmatrix}A_{1}&A_{2}&A_{3}\\B_{1}&B_{2}&B_{3}\\C_{1}&C_{2}&C_{3}\\\end{vmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d7af0616ddf13297024357fc90e030e39b4534)
